I am writing a program that takes raw double values from a database and converts them to 8-byte hex strings, but I don't know how to prevent loss of precision. The data recieved from all devices are stored as doubles, including the 8-byte identification values.
Instances of doubles such as 7.2340172821234e+16 parse correctly without loss of precision, where the exponent is 10^16.
However, in instances where the exponent is 10^17, Java loses precision. For example, 2.88512954935019e+17 is interpreted by Java as 1.44464854248327008E17
The code I am using looks like this:
public Foo(double bar) {
this.barString = Long.toHexString((long) bar);
if (barString.length == 15) {
barString = "0" + barString; //to account for leading zeroes lost on data entry
}
}
I am using a test case similar to this to test it:
@Test
public void testFooConstructor() {
OtherClass other = new OtherClass();
OtherClass.Foo test0 = other.new Foo(72340172821234000d); //7.2340172821234e+16
assertEquals("0101010100000150", test0.barString); //This test passes
OtherClass.Foo test1 = other.new Foo(144464854248327000d);//1.44464854248327e+17
assertEquals("02013e0500000758, test1.barString); //This test fails
}
The unit test states:
Expected: 02013e0500000758
Actual: 02013e0500000760
When I print out the values that Java stored 72340172821234000d and 144464854248327000d as it respectively prints:
7.2340172821234E16
1.44464854248327008E17
The latter value is off by 8, which seems to be consistent for the few that I have tested.
Is there anything I can do to correct this error?
EDIT: This is not a problem where I care about what is past the ones place. The question that some think this is a duplicate of is asking why floating point numbers are less precise, I am asking how to avoid the loss of precision, through similar workarounds to those that Roman Puchkovskiy suggested.

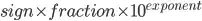
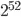 ) you will see you will get a 16 digits number. Double can represent bigger numbers than that by adding zeroes before or after using the number represented by the exponent, but it can't store number that have more than 16 digits without lose of precision.
) you will see you will get a 16 digits number. Double can represent bigger numbers than that by adding zeroes before or after using the number represented by the exponent, but it can't store number that have more than 16 digits without lose of precision.