If I understand your question, you want a line through your object where every point is in the middle of the object, i.e. if you start from any point on the midline and walk in a direction perpendicular to the midline, you have to walk the same distance in both directions until you meet the border of the object:
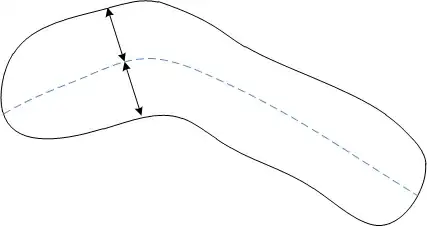
(this is just an illustration - probably not the geometrically correct midline!)
My quick&dirty solution would be to start with a middle axis (that can easily be calculated from first and second-order moments) and refine it by taking each point on this line and find the nearest border points on a line perpendicular to the current direction at that point, and move the point to the geometric center of these two points:

If you do this for every point, you should get a better approximation for the midline.
I said this was quick&dirty, because I'm not sure if simply repeating this procedure always converges to a stable solution. It probably depends on how you calculate the perpendicular direction of the midline in the presence of bends and kinks.
One way around this is to use a more physically-inspired model:
- Calculate a distance transform for the inside of your object (the distance of each point to the closest border point)
- Find a smooth line through the object that maximizes the path integral of the distance transform image:
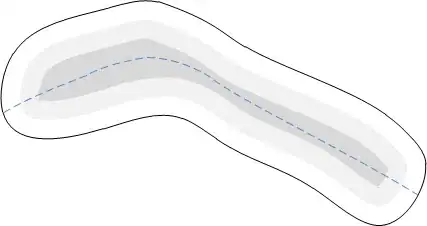
To find this line, I would use an algorithm similar to active contours/snakes:
- Start with the middle axis
- Apply two forces to each point:
- One force "pushes" the line in the direction of the gradient of the distance transform (i.e. away from the closest border)
- The other force counters the stretching and bending of the snake, so it keeps a smooth shape where there is no clear distance transform gradient. (Google for active contour - this is fairly standard CV stuff, you'll find lots of good articles about it.)
- Repeat until convergence or some fixed iteration limit is reached
You'll need to adjust a few parameters for these smoothness of the curve (as always with active contours), but your chances to get a well-defined and well-behaved approximation are far better than with the simple approach above.


