arbitrary operation on list

Question

["add",["subtract",["multiply",2,["add",1,3]], 4 ] , 5 ]

how can I do these operation

when prog see "add" it adds 1 and 3 and return 4 new list became

["add",["subtract",["multiply",2, 4 ], 4 ] , 5 ]

when prog see "multiply" it does 2*4 nd return 8 new list became

["add",["subtract",8, 4 ] , 5 ]

after one recursion

["add",4 , 5 ]

after last recursion

return 9

Is this homework? I can implement specifications for you, but that costs money. I'll also help you with a problem for fun, but you have to try by yourself first and actually run into problems. Otehrwise you won't learn. — Lennart Regebro, Dec 31 '10 at 09:42
I have tried to write with iteration but I failed so erased , now,again I am at start point.SO I have no code in my hand — , Dec 31 '10 at 09:43
@fatai: It looks exactly like homework. And we don't mind homework, but then you should tag it as homework. — Lennart Regebro, Dec 31 '10 at 09:47
The solution is a word you use in the question: *recursion*. — Andrew Jaffe, Dec 31 '10 at 09:48
@Ismail, your teacher I think a bit lazy, I have found this question in python book ( in exercise part ) — , Dec 31 '10 at 09:51
http://en.wikipedia.org/wiki/Reverse_Polish_notation#Postfix_algorithm — moinudin, Dec 31 '10 at 10:07

score 1 · Answer 1 · answered Dec 31 '10 at 09:49

1

You should write a recursive function that goes through the lists and do the operations.

It's actually fairly trivial, but I don't want to just hand you the answer, especially since it sounds like homework. :) So update your question with what you tried to do, and we'll tell you where you are going wrong.

answered Dec 31 '10 at 09:49

Lennart Regebro

167,292
41
224
251

can give me any example or page I will look them then I will try to write with recursion – Dec 31 '10 at 09:53
@fatai: Recusion is when you write a function that call itself. http://stackoverflow.com/questions/479343/how-can-i-build-a-recursive-function-in-python – Lennart Regebro Dec 31 '10 at 09:56

score 1 · Answer 2 · answered Dec 31 '10 at 11:59

1

import operator

def do_math(op):
    try:
        return getattr(operator, op[0][:3])(*[do_math(arg) for arg in op[1:]])
    except TypeError:
        return op

L = ["add",["subtract",["multiply",2,["add",1,3]], 4 ] , 5 ]
print do_math(L)

answered Dec 31 '10 at 11:59

nosklo

217,122
57
293
297

I think your program will crash , something like unary operator you forget to consider – Dec 31 '10 at 14:08
Not the way I'd write it (I am thinking about the try/except), but that's the idea. @gcc: why? unary operators should work fine. – tokland Dec 31 '10 at 14:41

Hugh Bothwell · Accepted Answer · 2011-01-01T03:44:52.867

The first thing to do is sketch it out visually as a tree:

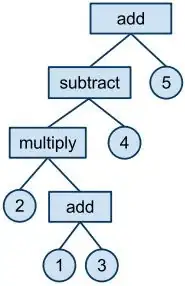
alt text

If you look at the left child (subtract, multiply / 4, etc) you see it is also a tree; and so is the left half of that (multiply, 2 / add, etc).

In fact, you can think of each node with its descendants as being a tree, consisting of either (a) an operator, with a left sub-tree and right sub-tree, or (b) a value (leaf node, no more descendants).

to evaluate a tree:
  if it is a value:
    you have the final value; return it
  otherwise, it is an operator:
    evaluate the left sub-tree
    evaluate the right sub-tree
    do operation(left-tree-value, right-tree-value)
    return the result

You will notice that 'evaluate tree' calls itself to operate on the sub-trees - this is recursion, where solving a problem depends on solving smaller versions of the same problem and then combining the results.

So the final evaluation order looks like:

what is tree value?
    add: {tree1} + {tree2}
    what is tree1?
        subtract: {tree3} - {tree4}
        what is tree3?
            multiply: {tree5} * {tree6}
            what is tree5?
            2
            what is tree6?
                add: {tree7} + {tree8}
                what is tree7?
                1
                what is tree8?
                3
                add: 1 + 3
            4
            multiply: 2 * 4
        8
        what is tree4?
        4
        subtract: 8 - 4
    4
    what is tree2?
    5
    add: 4 + 5
9

arbitrary operation on list

3 Answers3