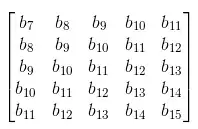I have a vectorb with 30 entries.
I want to avoid using a for loop to construct a matrix like this:
where b_i is the i-th entry of the vector b.
For example, define the vector
b = [2 6 -7 3 1 -4 -1 1 11 8 -4 9 2 0 2 -1 0 4 4 4 2 -4 2 5 1 3 2 -1 1 -2]
where I tried by using for loop is:
A = zeros(5,5);
for i = 1:5
A(i) = b(i+5);
A(i+5) = b(i+6);
A(i+10) = b(i+7);
A(i+15) = b(i+8);
A(i+20) = b(i+9);
end
The result is
Is there a faster and more general method to generate this matrix?