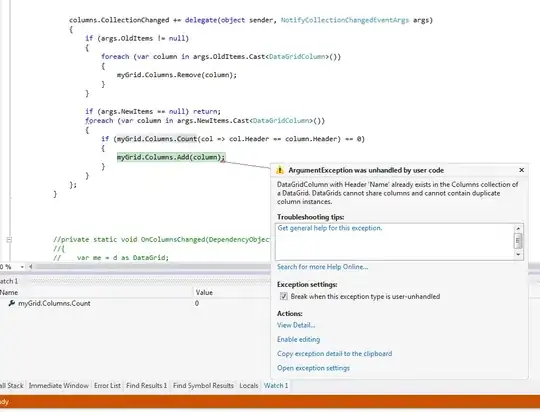
I have a dataframe:
Albedo Year_Since_Burn Summer_SRAD Winter_SRAD
1 397.00 1 17801.70 6589.56
2 289.60 2 18027.20 6633.96
3 615.29 3 17397.10 6952.69
4 258.12 4 17793.63 6627.62
5 139.32 5 17853.00 6675.00
6 463.81 6 17853.00 6675.00
7 532.47 7 17853.00 6675.00
8 300.09 8 17648.00 6890.00
9 118.00 9 17786.13 6724.67
10 238.18 10 18050.13 6916.46
11 439.11 11 18057.20 6893.08
12 366.00 12 17823.00 6618.12
13 441.25 13 17809.50 6673.79
14 450.31 14 17654.40 6849.19
15 275.43 15 17592.80 7202.88
16 147.11 16 17830.20 6672.88
17 285.68 17 18065.13 6897.58
18 309.61 18 17665.80 7036.62
19 264.95 19 18053.47 6867.17
20 125.18 20 17834.40 6661.19
21 289.50 21 17824.00 6684.50
22 293.61 22 17826.90 6681.83
23 368.95 23 17634.55 6914.06
24 563.11 24 17434.23 7043.04
25 434.41 25 17527.60 7070.38
26 199.78 26 17955.40 6704.00
27 153.37 27 17872.70 6637.00
28 287.29 28 17843.20 6659.67
29 173.52 29 17822.93 6616.75
30 239.28 30 17884.00 6580.56
31 292.91 31 17884.00 6580.56
32 323.00 32 18078.70 6758.50
33 282.00 33 18078.70 6758.50
34 237.50 34 17779.10 7303.38
35 225.00 35 17822.80 6617.42
36 237.55 36 17822.80 6617.42
37 247.11 37 17918.50 6695.71
38 336.48 38 17918.50 6695.71
39 290.00 39 17918.50 6695.71
40 248.42 40 17822.80 6617.42
41 304.74 41 17918.50 6695.71
42 311.52 42 17918.50 6695.71
43 281.39 43 17918.50 6695.71
44 234.68 44 17918.50 6695.71
45 297.58 45 17918.50 6695.71
46 265.52 46 17918.50 6695.71
47 186.29 47 17918.50 6695.71
48 291.16 48 17918.50 6695.71
49 185.17 49 17918.50 6695.71
50 288.94 50 17918.50 6695.71
51 269.64 51 17918.50 6695.71
52 255.00 52 17918.50 6695.71
I am fitting a GAM model in R like so:
gam.m1 <- gam(Albedo ~ s(Year_Since_Burn) + s(Summer_SRAD) + s(Winter_SRAD), data=df)
which seems to work fine, and returns result as I would expect.
I have now created some data to predict on. Essentially I randomly selected 2 rows in the original df, duplicated them 52 times each, and then removed the Year_Since_Burn and Albedo columns, and created some new Year_Since_Burn data. So I only manipulated one independent variable. I did this like so:
df <- df[sample(nrow(df), 2),]
df <- df %>% select (-c(Albedo, Year_Since_Burn))
#add an id columns
df$ID <- seq.int(nrow(df))
#loop through each row
for (i in 1:nrow(df)) {
#select each row
grp <- (df[i, ])
#repeat each row 52 times
grp <- grp[rep(seq_len(nrow(grp)), each=52),]
#add a column for year since burn
grp$Year_Since_Burn <- seq.int(nrow(grp))
#select rows to keep
grp <- grp %>% select (c(ID, Year_Since_Burn,Summer_SRAD, Winter_SRAD, Winter_Tavg, Summer_Tavg, PFI, Bulk_Density,
SOC_Content, SOC_Stock, L3_Ecoregion))
#append
combined[[i]] <- grp
}
#concat
final = do.call(rbind, combined)
Now for each unique ID in final I predicted the dependent variable like so:
y_hat <- predict(gam.m1, final)
and then I plotted to look at how the predictions varied with Year_Since_Burn:
final2 <- data.frame(as.array(final$ID), as.array(final$Year_Since_Burn), y_hat2)
names(final2) <- c("ID", 'Year_Since_Burn', "Predicted")
#plot
plots1 <- lapply(split(final2, final2$ID),
function(x)
ggplot(x, aes(x=Year_Since_Burn, y=Predicted)) +
geom_line())
For the output graphs the curves are identical in shape for every prediction, it is just the magnitudes that are shifting. I am not sure if this is what GAMs is supposed to do or if this is an error on my part. This is what the predictions for two different Id's look like: