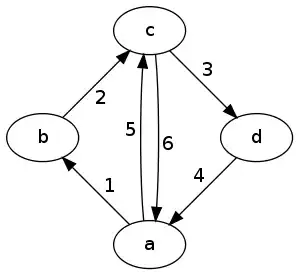
I had fun with this question, thanks! :P
I have a solution in C#. The algorithm to find the cycles is very short(~10 lines), but there is a lot of clutter around it(implementations of the classes Node and Edge for instance).
I've used the variable naming convention that the letter "e" represents an edge, the letter "a" the node where the edge start, and "b" the node it links to. With those conventions, this is the algorithm:
public static IEnumerable<Cycle> FindAllCycles()
{
HashSet<Node> alreadyVisited = new HashSet<Node>();
alreadyVisited.Add(Node.AllNodes[0]);
return FindAllCycles(alreadyVisited, Node.AllNodes[0]);
}
private static IEnumerable<Cycle> FindAllCycles(HashSet<Node> alreadyVisited, Node a)
{
for (int i = 0; i < a.Edges.Count; i++)
{
Edge e = a.Edges[i];
if (alreadyVisited.Contains(e.B))
{
yield return new Cycle(e);
}
else
{
HashSet<Node> newSet = i == a.Edges.Count - 1 ? alreadyVisited : new HashSet<Node>(alreadyVisited);
newSet.Add(e.B);
foreach (Cycle c in FindAllCycles(newSet, e.B))
{
c.Build(e);
yield return c;
}
}
}
}
It has an optimization to reuse some Hashsets, and that might be confusing. I've included the following code, which produces exactly the same results, but this implementation doesn't have optimizations, so you can figure out more easily how it works.
private static IEnumerable<Cycle> FindAllCyclesUnoptimized(HashSet<Node> alreadyVisited, Node a)
{
foreach (Edge e in a.Edges)
if (alreadyVisited.Contains(e.B))
yield return new Cycle(e);
else
{
HashSet<Node> newSet = new HashSet<Node>(alreadyVisited);
newSet.Add(e.B);//EDIT: thnx dhsto
foreach (Cycle c in FindAllCyclesUnoptimized(newSet, e.B))
{
c.Build(e);
yield return c;
}
}
}
This uses the following implementations of Node, Edge and Cycle. They're pretty straightforward, although I did put a lot of thought in making everything immutable and members as least accessible as possible.
public sealed class Node
{
public static readonly ReadOnlyCollection<Node> AllNodes;
internal static readonly List<Node> allNodes;
static Node()
{
allNodes = new List<Node>();
AllNodes = new ReadOnlyCollection<Node>(allNodes);
}
public static void SetReferences()
{//call this method after all nodes have been created
foreach (Edge e in Edge.AllEdges)
e.A.edge.Add(e);
}
//All edges linking *from* this node, not to it.
//The variablename "Edges" it quite unsatisfactory, but I couldn't come up with anything better.
public ReadOnlyCollection<Edge> Edges { get; private set; }
internal List<Edge> edge;
public int Index { get; private set; }
public Node(params int[] nodesIndicesConnectedTo)
{
this.edge = new List<Edge>(nodesIndicesConnectedTo.Length);
this.Edges = new ReadOnlyCollection<Edge>(edge);
this.Index = allNodes.Count;
allNodes.Add(this);
foreach (int nodeIndex in nodesIndicesConnectedTo)
new Edge(this, nodeIndex);
}
public override string ToString()
{
return this.Index.ToString();
}
}
public sealed class Edge
{
public static readonly ReadOnlyCollection<Edge> AllEdges;
static readonly List<Edge> allEdges;
static Edge()
{
allEdges = new List<Edge>();
AllEdges = new ReadOnlyCollection<Edge>(allEdges);
}
public int Index { get; private set; }
public Node A { get; private set; }
public Node B { get { return Node.allNodes[this.bIndex]; } }
private readonly int bIndex;
internal Edge(Node a, int bIndex)
{
this.Index = allEdges.Count;
this.A = a;
this.bIndex = bIndex;
allEdges.Add(this);
}
public override string ToString()
{
return this.Index.ToString();
}
}
public sealed class Cycle
{
public readonly ReadOnlyCollection<Edge> Members;
private List<Edge> members;
private bool IsComplete;
internal void Build(Edge member)
{
if (!IsComplete)
{
this.IsComplete = member.A == members[0].B;
this.members.Add(member);
}
}
internal Cycle(Edge firstMember)
{
this.members = new List<Edge>();
this.members.Add(firstMember);
this.Members = new ReadOnlyCollection<Edge>(this.members);
}
public override string ToString()
{
StringBuilder result = new StringBuilder();
foreach (var member in this.members)
{
result.Append(member.Index.ToString());
if (member != members[members.Count - 1])
result.Append(", ");
}
return result.ToString();
}
}
Then to illustrate how you might use this small API, I have implemented your two examples.
Basically it comes down to, create all the nodes by specifying to which nodes they link, then call SetReferences() to, well.... set some references. After that, calling the publicly accessible FindAllCycles() should return all cycles. I've excluded any code to reset the static members, but that is easily implemented. It should just clear all static lists.
static void Main(string[] args)
{
InitializeExampleGraph1();//or: InitializeExampleGraph2();
Node.SetReferences();
var allCycles = FindAllCycles().ToList();
}
static void InitializeExampleGraph1()
{
new Node(1, 2);//says that the first node(node a) links to b and c.
new Node(2);//says that the second node(node b) links to c.
new Node(0, 3);//says that the third node(node c) links to a and d.
new Node(0);//etc
}
static void InitializeExampleGraph2()
{
new Node(1);
new Node(0, 0, 2);
new Node(0);
}
I must note that the indices of the edges in these examples do NOT correspond to the indices in your images, but that is avoidable with a simple lookup.
The results: allCycles is for the first example:
{3, 2, 0}
{5, 4, 2, 0}
{3, 1}
{5, 4, 1}
allCycles is for the second example:
{1, 0}
{2, 0}
{4, 3, 0}
I hope you are satisfied with this solution and that you use it. I've barely commented on the code, so I know it might be hard to understand. In that case, please ask and I'll comment on it!