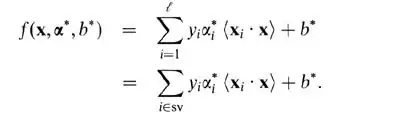Given a linearly separable dataset, is it necessarily better to use a a hard margin SVM over a soft-margin SVM?
-
1I think in the case linearly separable dataset, there is no need to SVM, SVM is useful when you have no good linearly separation of data. the honor of SVM is soft margins, in your case you didn't need it. – Saeed Amiri Jan 08 '11 at 12:35
2 Answers
I would expect soft-margin SVM to be better even when training dataset is linearly separable. The reason is that in a hard-margin SVM, a single outlier can determine the boundary, which makes the classifier overly sensitive to noise in the data.
In the diagram below, a single red outlier essentially determines the boundary, which is the hallmark of overfitting
To get a sense of what soft-margin SVM is doing, it's better to look at it in the dual formulation, where you can see that it has the same margin-maximizing objective (margin could be negative) as the hard-margin SVM, but with an additional constraint that each lagrange multiplier associated with support vector is bounded by C. Essentially this bounds the influence of any single point on the decision boundary, for derivation, see Proposition 6.12 in Cristianini/Shaw-Taylor's "An Introduction to Support Vector Machines and Other Kernel-based Learning Methods".
The result is that soft-margin SVM could choose decision boundary that has non-zero training error even if dataset is linearly separable, and is less likely to overfit.
Here's an example using libSVM on a synthetic problem. Circled points show support vectors. You can see that decreasing C causes classifier to sacrifice linear separability in order to gain stability, in a sense that influence of any single datapoint is now bounded by C.
Meaning of support vectors:
For hard margin SVM, support vectors are the points which are "on the margin". In the picture above, C=1000 is pretty close to hard-margin SVM, and you can see the circled points are the ones that will touch the margin (margin is almost 0 in that picture, so it's essentially the same as the separating hyperplane)
For soft-margin SVM, it's easer to explain them in terms of dual variables. Your support vector predictor in terms of dual variables is the following function.
Here, alphas and b are parameters that are found during training procedure, xi's, yi's are your training set and x is the new datapoint. Support vectors are datapoints from training set which are are included in the predictor, ie, the ones with non-zero alpha parameter.
- 10,348
- 5
- 39
- 36
- 57,332
- 22
- 139
- 197
-
Helped me very much! Can you explain the term "support vectors"? What is its meaning in SVM? – D.G Jan 08 '11 at 20:47
-
3The support vectors are just the points that are either misclassified or correctly classified but "close" to the decision plane. The decision rule is of the form f(x) = w dot x + b and most SVM formulations define a "close" x as abs(f(x)) < 1. – Davis King Jan 08 '11 at 21:43
-
@YaroslavBulatov, in your first figure, illustrating "hard margin" classifier, the blue line doesn't look like maximum margin hyperplane to me. If I make this line more horizontal, I will get larger margin. How did you get this "hard margin" hyperplane? – Leo Apr 10 '12 at 02:47
-
That's kind of an approximate diagram, I think you need some more blue points to make it precise – Yaroslav Bulatov Apr 24 '12 at 23:49
-
@Leo: The blue line is one of the two boundaries between which the maximum-margin hyperplane falls, not the maximum-margin hyperplane itself. We can see that the angle is sort of suboptimal, because the resulting maximum-margin hyperplane will not be orthogonal to the line connecting the centroids of the distributions. – Jun 02 '16 at 09:14
In my opinion, Hard Margin SVM overfits to a particular dataset and thus can not generalize. Even in a linearly separable dataset (as shown in the above diagram), outliers well within the boundaries can influence the margin. Soft Margin SVM has more versatility because we have control over choosing the support vectors by tweaking the C.
- 71
- 1
- 1