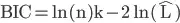optimum number of clusters in K mean clustering using BIC, (MATLAB)

Question

As you all know, in k-mean clustering we can use Bayesian Information Criterion (BIC) for finding out what is the optimum number of clusters. The k that minimizes the BIC score is the optimal number of clusters according to the BIC scoring scheme.

The formulation for BIC is as follows:

BIC(C) = n*ln(RSS/n) + k*ln(n)

where n is the number of data points in the data set and k is the number of clusters. RSS is Residual sum of squares where we sum the distance of each data point from the centroid of its own cluster. Our data contains 3100 points where each point has two elements y=(x1, x2) (Each entry has two features).

My code in Matlab is as follows:

BIC=[];% Bayesian Information Criterion 
n=3100; % number of datapoints
temp=1;  
for k=1:50  % number of clusters
    RSS=0;  % residual sum of squares
[idx,C]=kmeans(y,k);  % Matlab command for k-mean clustering
for i=1:3100
    RSS=RSS+sqrt((y(i,1)-C(idx(i),1))^2+(y(i,2)-C(idx(i),2))^2);
end
BIC(temp)=n*log(RSS/n)+k*log(n);
temp=temp+1;
end
[p,l]=min(BIC);
plot(BIC)

But something is definitely wrong here in my code and I cannot say what! I mean if we let k from 1 to 100 then the k that minimizes BIC will be 100. If we let k from 1 to 1000 then the k that minimizes BIC will be 1000 and so on and so forth. But as far as I know there should be a specific k that minimizes BIC. I appreciate your help

Your BIC equation is wrong? – Has QUIT--Anony-Mousse Sep 28 '17 at 19:53 — Has QUIT--Anony-Mousse, Sep 28 '17 at 19:53

score 1 · Accepted Answer · answered Sep 29 '17 at 19:08

I can see a couple of potential problems that could explain the behaviour you are reporting:

1) I believe you are using a siplified formula that is not appropriate for your case

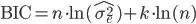I'm not sure about the specifics, but from wikipedia using the special case of $\mathrm{BIC} = n \cdot \ln(\widehat{\sigma_e^2}) + k \cdot \ln(n) \$ is only appropriate

Under the assumption that the model errors or disturbances are independent and identically distributed according to a normal distribution and that the boundary condition that the derivative of the log likelihood with respect to the true variance is zero

I am not well literate in the field yet to know whether the second condition holds. Looking at the formulas in the original X-means paper by Peleg and Moore following (this answer) I can see they did not reduce the formula to the one you are using (see page 4 in their linked paper for the full formulas. Note that they proposed a more sophisticated algorithm that considers at each iteration every centroid and its region against a couple of centroids for the same region and compares these two models using the BIC model selection. You'll have to change the formula in the paper to consider the whole of the model for a given k if you want to keep your approach).

2) You are confusing the k of two different contexts

You plugged the k from the k-means algorithm into the free-parameters penalising element of the formula.

From wikipedia

$\mathrm {BIC} ={\ln(n)k-2\ln({\hat {L}})}$

where

[...]

*k = the number of free parameters to be estimated.

In the above linked x-mean paper at the top of the second column in page 4 they calculate the number of free variables for a k-means model with k centroids in d-dimentional space to be k(d+1) which in your case gives 3k rather than k.

Changing your code in the line

BIC(temp)=n*log(RSS/n)+k*log(n);

into

BIC(temp)=n*log(RSS/n)+(k*3)*log(n);

and running it on a 1000 random-generated points in 2d I got a minimising k that is smaller than the maximum k (50):

optimum number of clusters in K mean clustering using BIC, (MATLAB)

1 Answers1