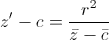0

I have 2 images that have same shapes present in them but are arranged at different places. I want to match those images correctly.

Steps performed...

  1. Get contour from Source Image.
  2. Get contours from target Image.
  3. Compare contours from source to target using Modified Hausdorff Distance.

  4. Get the smallest value as the match.

    def modified_hausdorff(A,B): D = cdist(A,B) #euclidean distance fhd = np.mean(np.min(D,axis=0)) rhd = np.mean(np.min(D,axis=1)) return max(fhd,rhd)

Source image.

Source image

Target image.

Target image

Micho
  • 3,929
  • 13
  • 37
  • 40
lakshay verma
  • 31
  • 3
  • And what's the problem exactly? – eshirima Oct 19 '17 at 13:58
  • The problem is that Modified Hausdorff Distances used the position to calculate the similarity between 2 shapes. As it calculates the distance between the set of points of shape A with Shape B. Therefore making it Translation Invariant. I need something to make this RSTInvariant. – lakshay verma Oct 23 '17 at 19:08
  • I faced a similar problem with regards to Hausdorff distance. To tackle translations, I translated all points; both template and frame, back to the origin. With regards to rotation, I rotated the frame points to match the angle of the template points. Scale, [image pyramids](https://en.wikipedia.org/wiki/Pyramid_(image_processing)) are your friend – eshirima Oct 23 '17 at 19:39
  • And uh, it'd be more helpful if you added the fact that you're looking for a Rotation, Scale and Translation Invariant solution. – eshirima Oct 23 '17 at 19:44
  • Thanks, @eshirima . Could you share your code or a snippet? That would be really helpful. I would be more careful next time to give complete detail of the problem. – lakshay verma Oct 24 '17 at 20:36

1 Answers1

1

This is a bi-directional task.

Forward Direction

1. Translation

For each contour, calculate its moment. Then for each point in that contour, translate it about the moment i.e. contour.point[i] = contour.point[i] - contour.moment[i]. This moves all of the contour points to the origin.

PS: You need to keep track of each contour's produced moment because it will be used in the next section

2. Rotation

With the newly translated points, calculate their rotated rect. This will give you the angle of rotation. Depending on this angle, you would want to calculate the new angle which you want to rotate this contour by; this answer would be helpful.

After attaining the new angle, calculate the rotation matrix. Remember that your center here will be the origin i.e. (0, 0). I did not take scaling into account (that's where the pyramids come into play) when calculating the rotation matrix hence I passed 1.

PS: You need to keep track of each contour's produced matrix because it will be used in the next section

Using this matrix, you can go ahead and rotate each point in the contour by it as shown here*.

Once all of this is done, you can go ahead and calculate the Hausdorff distance and find contours which pass your set threshold.

Back Direction

Everything done in the first section, has to be undone in order for us to draw the valid contours onto our camera feed.

1. Rotation

Recall that each detected contour produced a rotation matrix. You want to undo the rotation of the valid contours. Just perform the same rotation but using the inverse matrix.

For each valid contour and corresponding matrix
inverse_matrix = matrix[i].inv(cv2.DECOMP_SVD)
Use * to rotate the points but with inverse_matrix as parameter

PS: When calculating the inverse, if the produced matrix was not a square one, it would fail. cv2.DECOMP_SVD will produce an inverse matrix even if the original matrix was a non-square.

2. Translation

With the valid contours' points rotated back, you just have to undo the previously performed translation. Instead of subtracting, just add the moment to each point.

You can now go ahead and draw these contours to your camera feed.

Scaling

This is were image pyramids come into play.

All you have to do is resize your template image by a fixed size/ratio upto your desired number of times (called layers). The tutorial found here does a good job of explaining how to do this in OpenCV.

It goes without saying that the values you choose to resize your image by and number of layers will and do play a huge role in how robust your program will be.

Put it all together

Template Image Operations

Create a pyramid consisting of n layers
For each layer in n
    Find contours
    Translate the contour points
    Rotate the contour points

This operation should only be performed once and only store the results of the rotated points.

Camera Feed Operations

Assumptions

Let the rotated contours of the template image at each level be stored in templ_contours. So if I say templ_contours[0], this is going to give me the rotated contours at pyramid level 0.

Let the image's translated, rotated contours and moments be stored in transCont, rotCont and moment respectively.

image_contours = Find Contours
for each contour detected in image
    moment = calculate moment

for each point in image_contours
    transCont.thisPoint = forward_translate(image_contours.thisPoint)
    rotCont.thisPoint = forward_rotate(transCont.thisPoint)

for each contour_layer in templ_contours
    for each contour in rotCont
        calculate Hausdorff Distance
        valid_contours = contours_passing_distance_threshold

for each point in valid_contours
    valid_point = backward_rotate(valid_point)

for each point in valid_contours
    valid_point = backward_translate(valid_point)

drawContours(valid_contours, image)

It can be a little bit confusing at first especially with keeping track of every contours' respective moment and rotation matrices, but once you understand what is going on, it really is a very easy algorithm to implement.

eshirima
  • 3,837
  • 5
  • 37
  • 61