atan2f vs fmodf vs just plain subtraction

Question

I have a problem with a piece of code that I wrote to wrap an angle around during an integration and is part of a small simulation that I'm working on. So basically the idea is to prevent the angle from growing large by making sure that it always has a sane value. I have tried three different approaches that I would expect to give the same results. And most of the time they do. But the first two give artifacts around the point where angle value wraps around. When I then generate a waveform from the angle value I get undesirable results because of these precision errors.

So the first approach is like this (limit angle to -8PI +8PI range):

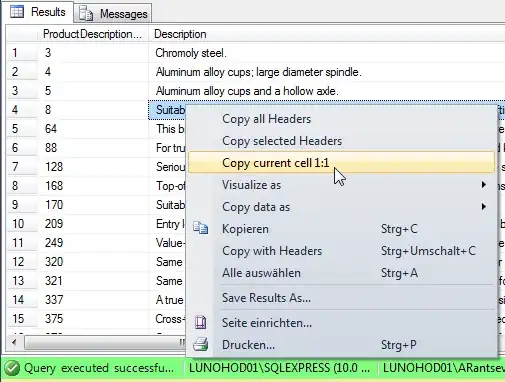
self->state.angle = atan2f(sinf(angle / 8), cosf(angle / 8)) * 8;

This creates artifact that looks like this:

Second approach of:

self->state.angle = fmodf(angle, (float)(2.f * M_PI * 8))

Creates the same result:

However if I just do it like this:

float limit = (8 * 2 * M_PI); 
if(angle > limit) angle -= limit;           
if(angle < 0) angle += limit;               
self->state.angle = a;

Then it works as expected without any artifacts:

So what am I missing here? Why do the other two approaches create precision error? I would expect all of them to generate the same result (I know that ranges of the angle are different but when the angle is passed further into a sin function I would expect the result to be the same).

Edit: small test

// g++ -o test test.cc -lm && ./test
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <stdint.h>

int main(int argc, char **argv){
    float a1 = 0;
    float a2 = 0;
    float a3 = 0;
    float dt = 1.f / 7500.f;

    for(float t = -4.f * M_PI; t < (4.f * M_PI); t+=dt){
        a1 += dt;
        a2 += dt;
        a3 += dt;

        float b1 = a1;
        if(b1 > 2.f * M_PI) b1 -= 2.f * M_PI;
        if(b1 < 0.f) b1 += 2.f * M_PI;
        float b2 = atan2f(sinf(a2), cosf(a2));
        float b3 = fmodf(a3, 2 * M_PI);

        float x1 = sinf(b1);
        float x2 = sinf(b2);
        float x3 = sinf(b3);

        if((x1 * x2 * x3) > 1e-9){
            printf("%f: x[%f %f %f],\tx1-x2:%f x1-x3:%f x2-x3:%f]\n", t, x1, x2, x3, (x1 - x2) * 1e9, (x1 - x3) * 1e9, (x2 - x3) * 1e9);
        }
    }

    return 0;
}

Output:

-9.421306: x[0.001565 0.001565 0.001565],       x1-x2:0.000000 x1-x3:0.000000 x2-x3:0.000000]
-9.421172: x[0.001431 0.001431 0.001431],       x1-x2:0.000000 x1-x3:0.000000 x2-x3:0.000000]
-9.421039: x[0.001298 0.001298 0.001298],       x1-x2:0.000000 x1-x3:0.000000 x2-x3:0.000000]
-9.420905: x[0.001165 0.001165 0.001165],       x1-x2:0.000000 x1-x3:0.000000 x2-x3:0.000000]
-9.420772: x[0.001032 0.001032 0.001032],       x1-x2:0.000000 x1-x3:0.000000 x2-x3:0.000000]
-6.275573: x[0.001037 0.001037 0.001037],       x1-x2:0.000000 x1-x3:174.855813 x2-x3:174.855813]
-6.275439: x[0.001171 0.001171 0.001171],       x1-x2:0.000000 x1-x3:174.855813 x2-x3:174.855813]
-6.275306: x[0.001304 0.001304 0.001304],       x1-x2:0.000000 x1-x3:174.855813 x2-x3:174.855813]
-6.275172: x[0.001438 0.001438 0.001438],       x1-x2:0.000000 x1-x3:174.855813 x2-x3:174.855813]
-6.275039: x[0.001571 0.001571 0.001571],       x1-x2:0.000000 x1-x3:174.855813 x2-x3:174.855813]
-6.274905: x[0.001705 0.001705 0.001705],       x1-x2:0.000000 x1-x3:174.855813 x2-x3:174.855813]
-6.274772: x[0.001838 0.001838 0.001838],       x1-x2:0.116415 x1-x3:174.855813 x2-x3:174.739398]

`if(angle > limit) angle -= limit; ` is not `while(angle > limit) angle -= limit; ` so basically if `angle = 800000 * M_PI` your last method does not put your value in range. a [mcve] could be useful, with input values, expected, and "unexpected" using `fmod` (forget `atan2f` ATM) — Jean-François Fabre, Oct 17 '17 at 15:20
The screenshot does not appear to be made on a machine that is going to suffer at all when you use *double* instead of *float*. — Hans Passant, Oct 17 '17 at 15:47
The code will run on embedded target with only 32 bit float support. — Martin, Oct 17 '17 at 15:48
By subtracting out `M_PI` instead mathematical π, you introduce a small phase error that grows with every additional subtraction of `M_PI`. It is not clear what the exact context of this computation is, but usually it is a red flag when a computation involves evaluating trig functions for large argumentd. Consider representing the angle as a double-`float` to double the precision during accumulation, or check whether use of the `sinpi()` and `cospi()` [functions](https://stackoverflow.com/questions/42792939/implementation-of-sinpi-and-cospi-using-standard-c-math-library) may be applicable — njuffa, Oct 17 '17 at 22:34

Jean-François Fabre · Accepted Answer · 2017-10-18T08:07:13.863

Without more information it's difficult to provide an explanation but I'll try anyway.

The difference between using fmod and "plain subtraction" (or addition) like you're doing is that if the value is way out of range already (like 800000 * M_PI for instance), then the add/subtract method doesn't change the value much (it has little effect) and a very big (in absolute value) angle hits your computation function, without an issue, since no artifact is seen.

Using fmod (or atan2) guarantees that the value is in the range you defined, which isn't the same thing.

Note that doing:

float limit = (8 * 2 * M_PI); 
while(angle > limit) angle -= limit;           
while(angle < 0) angle += limit;               
self->state.angle = a;

would be equivalent (roughly) to fmod (but would be worse than fmod for big values since it introduces floating point accumulation errors because of repeated additions or subtractions).

So if inputting very big values in your computation produces the correct result, then you can wonder if it's wise to normalize your angles instead of leaving that to the math library.

EDIT: the first part of this answer assumed that this super-out-of-bounds case would happen, and further question edits showed that this wasn't the case, so...

The other difference between fmod and 2 tests is that there's no guaranteed that the value is the same if already in range when calling fmod

For instance if the implementation is like value - int(value/modulus)*modulus;, floating point inaccuracy may substract a small value to the original value.

Using atan2f combined with sin ... also changes the result if already in range.

(and even if the value is slightly out of range, adding/subbing like you're doing doesn't involve dividing/truncating/multiplying)

Since you can adjust the value in the range by just adding or subbing once, using fmodf or atan2f is overkill in your case, and you can stick to your simple sub/add (adding an else would save a test: if you just reajusted a too low value, no need to test to see if the value is too big)

Yes of course. I'm just trying to figure out why the different result given examples above. The purpose is to just keep the angle from going out into infinity so snapping it in range in one go is not necessary since during each iteration it never moves more than 0.5PI. — Martin, Oct 17 '17 at 16:05
Added a small example. It is apparent that there are small differences in the order of 1e-6 values. It could be that these small changes get amplified and create substantial errors after several matrix multiplications and integrations. I'm still trying to pinpoint exactly what could be causing the problem when using atan2/fmodf.. — Martin, Oct 17 '17 at 16:54
ok, I' ve enhanced my answer. Still can't pinpoint the root cause, but tries to explain and justify your design choice. — Jean-François Fabre, Oct 17 '17 at 19:56

chux - Reinstate Monica · Answer 2 · 2017-10-18T18:42:53.857

3

float versus double math.

Of course the 3rd method works best. It is using double math.

Look at b1, b3. b3 is certainly calculated with float precision due to the fmodf() call.

Note that M_PI is usually a double, so b1 -= 2.f * M_PI; is likely done with double precision math and provides a more accurate answer. The f in 2.f does not force the product 2.f * M_PI into float - the product is double and so is -=.

b1 -= 2.f * M_PI;
// same as 
b1 = (float)((double)b1 - (2.f * M_PI));

Further: with optimizations and FLT_EVAL_METHOD > 0, C is allowed to perform FP code at higher than the precision of the type. b1 may calculate at double, even though code appears float. With higher precision, and the fact that M_PI (a rational number) is not exactly π (an irrational number), leads to a more accurate b1 than fmodf(a3, 2 * M_PI);

float b1 = a1;
if(b1 > 2.f * M_PI) b1 -= 2.f * M_PI;  // double math
if(b1 < 0.f) b1 += 2.f * M_PI;         // double math
float b3 = fmodf(a3, 2 * M_PI);

To insure float results, use volatile float b1 = a1; to do a fair comparison and use float constants like #define M_PIf ((float) M_PI)

Further. With a fair comparison, better to use if(b1 < -2.f * M_PIf) b1 += 2.f * M_PIf;

Recommend OP print FLT_EVAL_METHOD to aid further discussion.

#include <float.h>
printf("%d\n", FLT_EVAL_METHOD);

OP has 2 solutions:

Use wider math like double for the sensitive radian reduction.
```
float b3 = fmod(a3, 2 * M_PI);  // not fmodf
```
Do not use radians, but an angle measurement like degrees or BAM and perform exact range reduction. Angles will need degrees to radian conversions prior to trig calls.
```
float b3 = fmodf(a3, 360.0f);  // use fmodf, a3, b3 are in degrees
```

Note: the float b2 = atan2f(sinf(a2), cosf(a2)); method is not a reasonable contender.

edited Oct 18 '17 at 18:42

answered Oct 18 '17 at 13:27

chux - Reinstate Monica

143,097
13
135
256

With respect to your last point, I had suggested looking into the use of `sinpi()` and `cospi()` in comments, which implies treating the angles as fractions of π, and makes full-circle wrapping exact within a very large range, – njuffa Oct 18 '17 at 17:18
@njuffa Thanks. `sinpi(), cospi()` are useful, yet unfortunately they are not yet part of the standard C library. – chux - Reinstate Monica Oct 18 '17 at 18:38
That's why I posted reasonable C implementations of them in honor of this year's π-day [here](https://stackoverflow.com/questions/42792939/implementation-of-sinpi-and-cospi-using-standard-c-math-library). – njuffa Oct 18 '17 at 19:01
@njuffa Your good code relies heavily on `fma()`, yet `fma()` is [not always well implemented](https://stackoverflow.com/q/42166563/2410359) which defeats the value of these `sinpi(), cospi()` - still good idea. – chux - Reinstate Monica Oct 18 '17 at 20:08
I am aware of that, but hardware support for FMA is available on all major architectures now, so my work is always forward looking. – njuffa Oct 18 '17 at 20:16
@njuffa Hardware support may be available, as it is on my machine, yet if the library does not use it, it might as well not exist. The library implementors simply fell short of a quality implementation for this present day library. It certainly is not your fault weak `fma()` exists - I am just pointing out weak ones do exist today - even when not expected. – chux - Reinstate Monica Oct 18 '17 at 20:22
The thread you pointed to is quite old. I am under the impression *that at this point in time* commonly used libraries that expose `fma()` use the FMA instruction provided by the hardware where it exists (which is almost everywhere now) and otherwise provide good software emulation. – njuffa Oct 18 '17 at 20:30
Let us [continue this discussion in chat](http://chat.stackoverflow.com/rooms/157029/discussion-between-chux-and-njuffa). – chux - Reinstate Monica Oct 18 '17 at 20:39

atan2f vs fmodf vs just plain subtraction

2 Answers2