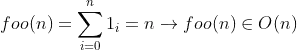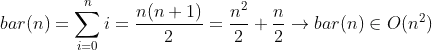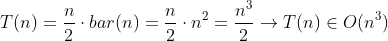Find the time complexity and big O of following code. I am confused about what will be the time complexity of if else statements and other bar(a) and foo(a) function. Some friends are saying its time complexity is O(n^2) and some says its time complexity will be O(n). I also think that the time complexity of the following code will be O(n) because there is a return statement in the for loops which will make the time of both foo and bar function as O(1) and main for loop will run n time so time complexity will be O(n).
// Sample Code
public static void main(String args[]){
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int sum = 0;
for(int i=0 ; i<n ; ++i){
if(i%2 != 0){
sum += foo(i , n) + foo(1+i , n);
}
else{
sum += foo(i , n) + bar(i , n);
}
}
}
-
static void bar(int a , int n){
for(int i=0 ; i<n ; ++i){
for(int j=0 ; j< i ; ++j){
return a*(i+j);
}
}
}
-
static void foo(int a , int n){
for(int i=0 ; i<n ; ++i){
return a*i;
}
}