Solving ODEs - only positive solutions

Question

I am trying to to solve ODEs restricted to positive solutions, i.e.:

dx/dt=f(x)

with x>=0.

In MATLAB this is very easy to implement. Is there any workaround or package for R to restrict the solution-space to positive values only?

This is very crucial in my case and unfortunately there is no alternative. I searched for a while now but without any success. :-(

Answer 1

There's still not quite enough to go on here. For the sorts of problems I'm familiar with, modifying the system to operate on the scale of the log-transformed state variables works well (you can always back-transform the results e.g. to compare them with data). I have used this, for example, with the SIR model in epidemiology. I'm going to try with @MauritsEver's example, to illustrate transforming the system to operate on the log scale:

library(deSolve)
model <- function (time, y, parms) {
   with(as.list(c(y, parms)), {
       dlogN <-   r * (1 - exp(logN) / K)
       list(dlogN)
   })
}

# Starting conditions
y <- c(logN = log(0.1))
parms <- c(r = 0.1, K = 10)
times <- seq(0, 100, 1)
out <- as.data.frame(ode(y, times, model, parms))
out_backtran <- transform(out,N=exp(logN))
plot(N~time,data=out_backtran)

This approach has the following disadvantages:

• it won't handle solutions that are exactly on the boundary, and will have trouble with solutions that approach the boundary "too fast" (i.e. where state variables converge to zero in finite time)
• as written it requires manual translation. It would be entirely possible to write a system that allowed the user to enter a set of equations and a set of transformations and applied the transformations automatically, but it would be some effort.
• It may increase computational effort slightly (any time we have to use the original-scale value of the state variable we have to exponentiate)

Answer 2

Without any specific example code or details on the ODE it's difficult to be more specific. It could be quite simple, depending on the problem.

Here is a trivial example using deSolve and its function deSolve::subset.

# Example straight from the deSolve manual
library(deSolve);
model <- function (time, y, parms) {
    with(as.list(c(y, parms)), {
        dN <-   r * N * (1 - N / K);
        list(dN)
    })
}

# Starting conditions
y <- c(N = 0.1);
parms <- c(r = 0.1, K = 10);
times <- seq(0, 100, 1);

# Solve ODE and plot
out <- ode(y, times, model, parms);
plot(out, type = "l", xlim = c(0, 100));

We now impose a constraint on time and subset the solution.

# Constrain: time > 20 and plot
out.constrained <- subset(out, select = c("time", "N"), subset = time > 20);
plot(out.constrained, type = "l", xlim = c(0, 100));

Answer 3

I think I have the same problem and might provide you an example.

Consider a dissolution process where a product A_solid dissolve into A_bulk at rate constant k_1 in a solvent (this reaction can go in the two directions). A_solid dissolves into the solvent until A_bulk reaches the saturation A_sat. Moreover A_bulk reacts with a product B to give C at a rate constant k_2. This is the picture of the reaction:

Dissolution process

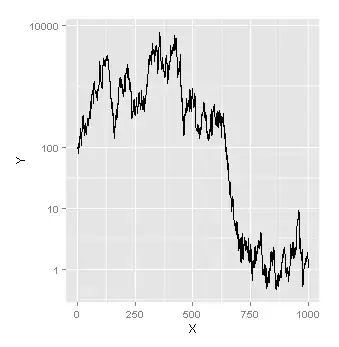This is the code I have written for the reaction:

library(deSolve)

# inputs 
T = 0  + 273.15 # K (Kelvin ) / tTemperature 
V = 50 # mL / Volume
A_solid = 125/V # mmol/mL = mol/L / initial concentration of product A_solid
B = 100/V # mol/L / initial concentration of product B

# parameters
R = 8.314 # J/(K*mol) / gas constant
expfact_sat = 2
E_a_sat = 10^3

params <- c(k1 = 0.1, # rate constant of dissolution
            k2 = 3*10^(-3), # rate constant of reaction
            A_sat = expfact_sat*exp(-E_a_sat/(R*T))) # saturation of the A_bulk into the solvent

# initial values
state <- c(A_solid = A_solid, A_bulk = 0, B = B, C = 0)

# system of differential equations
derivs <- function(t, y, parms) {
  with(as.list(c(y, parms)), {
    dA_solid = -k1*(A_sat - A_bulk)
    dA_bulk = -k2*A_bulk*B + k1*(A_sat - A_bulk)
    dB = -k2*A_bulk*B
    dC = k2*A_bulk*B
    return(list(c(dA_solid, dA_bulk, dB, dC)))
  })                                                        
}

times = seq(0, 500, by = 0.01)
init <- ode(y = state, func = derivs, time = times, parms = params)

l = dim(init)[1]-1
matplot(init[,1], init[,-1], type = "l", lty = 1:1, lwd = c(2),
        col = 1:l, xlab = "time [min]", ylab = "concn [mol/L]")
legend("topright", colnames(init)[-1], col = 1:l, lwd = c(2))

The problem here is that if you make the plot you will see that A_solid is going under 0, which means that the concentration of A_solid is negative, which is non-sense.

This is how the final plot should look like:

Dissolution

If you have any advice or solution how to handle this problem, this would be nice.

@BenBolker: The problem with the log transformation is, as you stated in your disadvantages, the concentration of A_solid goes in finite time to 0, and so I am not sure that we can still apply this technique.

P.S.: I am new to this forum and so I cannot display the images directly.

Answer 4

@Anto Add in an if statement to set it equal to zero

dA_solid = -k1*(A_sat - A_bulk)
if((A_solid+dA_solid)<0 {dA_solid = -1*(A_solid)}
dA_bulk = -k2*A_bulk*B + k1*(A_sat - A_bulk)