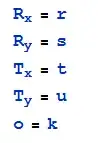How can I have a constrained Finite State Machine in Haskell / Idris?

Question

EDIT: Users @apocalisp and @BenjaminHodgson left awesome answers below, skip reading most of the question and jump to their answers.

TLDR of the Question: How can I go from the first picture, where FSM states combinatorial explode, to the second picture, where you're just required to visit all of them before moving on.

---

I would like to build a Finite State Machine (in Haskell really, but I'm trying Idris first to see if it can guide my Haskell) where there are some interim states that must be visited before a final state can be reached. It'd be great if I could arbitrarily constrain the FSM with predicates on some state.

In the following picture, there's an Initial state, 3 interim states A, B, C, and a Final state. If I'm not mistaken, in a "normal" FSM, you will always need n! interim states to represent each combination of possible paths.

This is undesirable.

Instead, using Type Families, and maybe Dependent types, I think it should be possible to have a sort of state that is carried around, and only when it passes certain predicates will you be allowed to travel to the final state. (Does that make it Push Down Automata instead of FSM?)

My code so far (idris), which by analogy, is adding ingredients to make a salad, and the order doesn't matter, but they all need to make it in:

data SaladState = Initial | AddingIngredients | ReadyToEat

record SaladBowl where
       constructor MkSaladBowl
       lettuce, tomato, cucumber : Bool

data HasIngredient : (ingredient : SaladBowl -> Bool) -> (bowl : SaladBowl ** ingredient bowl = True) -> Type where
     Bowl : HasIngredient ingredient bowl

data HasIngredients : (ingredients : List (SaladBowl -> Bool))
                     -> (bowl : SaladBowl ** (foldl (&&) True (map (\i => i bowl) ingredients) = True)) 
                     -> Type where
     Bowlx : HasIngredients ingredients bowl

data SaladAction : (ty : Type) -> SaladState -> (ty -> SaladState) -> Type where
     GetBowl     : SaladAction SaladBowl Initial (const Initial)
     AddLettuce  : SaladBowl -> SaladAction (bowl ** HasIngredient lettuce bowl)  st (const AddingIngredients)
     AddTomato   : SaladBowl -> SaladAction (bowl ** HasIngredient tomato bowl)   st (const AddingIngredients)
     AddCucumber : SaladBowl -> SaladAction (bowl ** HasIngredient cucumber bowl) st (const AddingIngredients)
     MixItUp     : SaladBowl -> SaladAction (bowl ** (HasIngredients [lettuce, tomato, cucumber] bowl)) AddingIngredients (const ReadyToEat)
     Pure : (res : ty) -> SaladAction ty (state_fn res) state_fn
     (>>=) : SaladAction a state1 state2_fn
           -> ((res : a) -> SaladAction b (state2_fn res) state3_fn)
           -> SaladAction b state1 state3_fn

emptyBowl : SaladBowl
emptyBowl = MkSaladBowl False False False

prepSalad1 : SaladAction SaladBowl Initial (const ReadyToEat)
prepSalad1 = do
           (b1 ** _) <- AddTomato emptyBowl
           (b2 ** _) <- AddLettuce b1
           (b3 ** _) <- AddCucumber b2
           MixItUp b3

And counter example programs that the compiler should error on:

BAD : SaladAction SaladBowl Initial (const ReadyToEat)
BAD = do
           (b1 ** _) <- AddTomato emptyBowl
           (b2 ** _) <- AddTomato emptyBowl
           (b3 ** _) <- AddLettuce b2
           (b4 ** _) <- AddCucumber b3
           MixItUp b4

BAD' : SaladAction SaladBowl Initial (const ReadyToEat)
BAD' = do
           (b1 ** _) <- AddTomato emptyBowl
           MixItUp b1

I eventually want the "ingredients" to be Sums instead of Bools (data Lettuce = Romaine | Iceberg | Butterhead), and more robust semantics where I can say things like "you must first add lettuce, or spinach, but not both".

Really, I feel so quite thoroughly lost, that I imagine my above code has gone in the completely wrong direction... How can I build this FSM (PDA?) to preclude bad programs? I'd especially like to use Haskell for it, perhaps using Indexed Monads?

Answer 1

The indexed state monad does exactly this.

The regular State s monad models a state machine (a Mealy machine, specifically) whose state alphabet is the type s. This data type is really just a function:

newtype State s a = State { run :: s -> (a, s) }

A function of type a -> State s b is a machine with input alphabet a and output alphabet b. But it's really just a function of type (a, s) -> (b, s).

Lining up the input type of one machine and output type of another machine, we can compose two machines:

(>>=) :: State s a -> (a -> State s b) -> State s b
m >>= f = State (\s1 -> let (a, s2) = run m s1 in run (f a) s2)  

In other words, State s is a monad.

But sometimes (as in your case), we need the type of the intermediate states to vary. This is where the indexed state monad comes in. It has two state alphabets. IxState i j a models a machine whose start state must be in i and end state will be in j:

newtype IxState i j a = IxState { run :: i -> (a, j) }

The regular State s monad is then equivalent to IxState s s. We can compose IxState as easily as State. The implementation is the same as before, but the type signature is more general:

(>>>=) :: IxState i j a -> (a -> IxState j k b) -> IxState i k b
m >>>= f = IxState (\s1 -> let (a, s2) = run m s1 in run (f a) s2)  

IxState is not exactly a monad, but an indexed monad.

We now just need a way of specifying constraints on the type of our state. For the salad example, we want something like this:

mix :: IxState (Salad r) Ready ()

This is a machine whose input state is some incomplete Salad consisting of ingredients r, and whose output state is Ready indicating that our salad is ready to eat.

Using type-level lists, we could say this:

data Salad xs = Salad
data Ready = Ready
data Lettuce
data Cucumber
data Tomato

The empty salad has an empty list of ingredients.

emptyBowl :: IxState x (Salad '[]) ()
emptyBowl = iput Salad

We can add Lettuce to any Salad:

addLettuce :: IxState (Salad r) (Salad (Lettuce ': r)) ()
addLettuce = iput Salad

And we can repeat the same for Tomato and Cucumber.

Now the type of mix just needs to be:

mix :: IxState (Salad '[Lettuce, Cucumber, Tomato]) Ready ()
mix = const Ready

We'll get a type error if we try to mix any salad that we haven't added Lettuce, Cucumber, and Tomato to, in that order. E.g. this will be a type error:

emptyBowl >>>= \_ -> addLettuce >>>= \_ -> mix

But ideally we'd like to be able to add the ingredients in any order. So we need a constraint on our type-level list asking for evidence that a particular ingredient is somewhere in our salad:

class Elem xs x

instance {-# OVERLAPS #-} Elem (x ': xs) x
instance Elem xs x => Elem (y ': xs) x

Elem xs x is now evidence that the type x is in the type-level list xs. The first instance (the base case) says that x is obviously an element of x ': xs. The second instance says that if the type x is an element of xs, then it's also an element of y ': xs for any type y. OVERLAPS is necessary to make sure Haskell knows to check the base case first.

Here's the complete listing:

{-# LANGUAGE TypeOperators #-}
{-# LANGUAGE DataKinds #-}
{-# LANGUAGE MultiParamTypeClasses #-}
{-# LANGUAGE PolyKinds #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE FlexibleContexts #-}

import Control.Monad.Indexed
import Control.Monad.Indexed.State

data Lettuce
data Tomato
data Cucumber

data Ready = Ready

class Elem xs x

instance {-# OVERLAPS #-} Elem (x ': xs) x
instance Elem xs x => Elem (y ': xs) x

data Salad xs = Salad

emptyBowl :: IxState x (Salad '[]) ()
emptyBowl = iput Salad

addLettuce :: IxState (Salad r) (Salad (Lettuce ': r)) ()
addLettuce = iput Salad

addTomato :: IxState (Salad r) (Salad (Tomato ': r)) ()
addTomato = iput Salad

addCucumber :: IxState (Salad r) (Salad (Cucumber ': r)) ()
addCucumber = iput Salad

mix :: (Elem r Lettuce, Elem r Tomato, Elem r Cucumber)
    => IxState (Salad r) Ready ()
mix = imodify mix'
  where mix' = const Ready

x >>> y = x >>>= const y

-- Compiles
test = emptyBowl >>> addLettuce >>> addTomato >>> addCucumber >>> mix

-- Fails with a compile-time type error
fail = emptyBowl >>> addTomato >>> mix

Answer 2

Your question is a little vague, but I read it as "how can I incrementally build a heterogeneous 'context' and create a record once I have values of the correct types in scope?" Here's how I'd skin this particular cat: rather than threading input and output types through some monadic context, let's just work with ordinary functions. If you want to use clever type-level machinery, you can use it with the values you pass around, rather than structure your program around a particular notion of computation.

Enough waffling. I'm going to represent a heterogeneous context as a nested tuple. I'll use the unit (()) to represent an empty context, and I'll add types to the context by nesting the context into the left element of a new tuple. So, a context containing an Int, a Bool and a Char looks like this:

type IntBoolChar = ((((), Int), Bool), Char)

Hopefully you can see how you'd incrementally add ingredients to a salad bowl:

-- we will *not* be using this type like a state monad
addLettuce :: a -> (a, Lettuce)
addLettuce = (, Romaine)

addOlives :: a -> (a, Olive)
addOlives = (, Kalamata)

addCheese :: a -> (a, Cheese)
addCheese = (, Feta)

addGreekSaladIngredients :: a -> (((a, Lettuce), Olive), Cheese)
-- yes, i know you also need tomatoes and onions for a Greek salad. i'm trying to keep the example short
addGreekSaladIngredients = addCheese . addOlives . addLettuce

This is not advanced type magic. It'll work in any language with tuples. I've even designed real-world APIs around this idea in C#, to partially compensate for C#'s lack of currying when you might use Applicative syntax in Haskell. Here's an example from my parser combinator library: starting with an empty permutation parser, you Add a number of atomic parsers of different types, and then Build a parser which runs those parsers in an order-insensitive manner, returning a nested tuple of their results which you can then flatten by hand.

---

The other half of the question was about turning a value of this sort of context into a record.

data Salad = Salad {
    _lettuce :: Lettuce,
    _olive :: Olive,
    _cheese :: Cheese
}

You can generically map nested tuples onto a record like this in an order-insensitive way using the following simple class:

class Has a s where
    has :: Lens' s a

-- this kind of function can be written generically using TH or Generics
toSalad :: (Has Lettuce s, Has Olive s, Has Cheese s) => s -> Salad
toSalad x = Salad (x^.has) (x^.has) (x^.has)

(This is a straightforward generalisation of the HasX classes that lens generates with Template Haskell.)

The only part which requires some type cleverness is automatically instantiating Has for nested tuples. We need to distinguish between two cases: either an item of the type we're looking for is on the right of a pair, or it's somewhere inside the nested tuple on the left of the pair. The problem is that under ordinary circumstances these two cases look the same to the elaborator: instance resolution occurs by a simple-minded process of syntactic type matching; type equalities aren't inspected and backtracking doesn't happen.

The upshot is that we need The Advanced Overlap Trick. Briefly, the trick uses a closed type family to dispatch a type class based on a type equality. We're choosing between two alternatives, so this is one of the few cases when a type-level boolean is acceptable.

type family Here a as where
    Here a (_, a) = True
    Here a (_, b) = False

class Has' (here :: Bool) a s where
    has' :: Proxy here -> Lens' s a

instance Has' True a (as, a) where
    has' _ = _2
instance Has a as => Has' False a (as, b) where
    has' _ = _1.has

instance Has' (Here a (as, b)) a (as, b) => Has a (as, b) where
    has = has' (Proxy :: Proxy (Here a (as, b)))

This program will stop the search at the first matching type. If you need two different types of lettuce in your salad, you'll have to wrap one in a newtype. In practice, when you combine this disadvantage with the complexity of the overlapping instances, I'm not convinced the Has abstraction pays its way. I'd just flatten the tuple by hand:

toSalad :: (((a, Lettuce), Olive), Cheese) -> Salad
toSalad (((_, l), o), c) = Salad l o c

You do lose order-insensitivity though.

Here's an example usage:

greekSalad = toSalad $ addGreekSaladIngredients ()

ghci> greekSalad
Salad {_lettuce = Romaine, _olive = Kalamata, _cheese = Feta}  -- after deriving Show

---

And here's the completed program

{-# LANGUAGE UndecidableInstances #-}
{-# LANGUAGE TupleSections #-}
{-# LANGUAGE FlexibleContexts #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE RankNTypes #-}
{-# LANGUAGE MultiParamTypeClasses #-}
{-# LANGUAGE TypeFamilies #-}
{-# LANGUAGE DataKinds #-}
{-# LANGUAGE TypeInType #-}
{-# LANGUAGE ScopedTypeVariables #-}

import Control.Lens hiding (has, has')
import Data.Proxy

data Lettuce = Romaine deriving (Show)
data Olive = Kalamata deriving (Show)
data Cheese = Feta deriving (Show)

data Salad = Salad {
    _lettuce :: Lettuce,
    _olive :: Olive,
    _cheese :: Cheese
} deriving (Show)

-- we will *not* be using this type like a state monad
addLettuce :: a -> (a, Lettuce) -- <<< Tuple Sections
addLettuce = (, Romaine)

addOlives :: a -> (a, Olive)
addOlives = (, Kalamata)

addCheese :: a -> (a, Cheese)
addCheese = (, Feta)

addGreekSaladIngredients :: a -> (((a, Lettuce), Olive), Cheese)
addGreekSaladIngredients = addCheese . addOlives . addLettuce

class Has a s where
  has :: Lens' s a

type family Here a as where
    Here a (_, a) = True
    Here a (_, b) = False

class Has' (here :: Bool) a s where
    has' :: Proxy here -> Lens' s a

instance Has' True a (as, a) where
    has' _ = _2

instance Has a as => Has' False a (as, b) where
    has' _ = _1.has

instance  Has' (Here a (as, b)) a (as, b) => Has a (as, b) where -- <<< Undecidable Instances
    has = has' (Proxy :: Proxy (Here a (as, b)))

toSalad :: (Has Lettuce s, Has Olive s, Has Cheese s) => s -> Salad
toSalad x = Salad (x ^. has) (x ^. has) (x ^. has)

greekSalad = toSalad $ addGreekSaladIngredients ()

-- nonSaladsError = toSalad $ (addCheese . addOlives) ()