Eigen vectors in python giving seemingly random element-wise signs

Question

I'm running the following code:

import numpy as np
import matplotlib
matplotlib.use("TkAgg")
import matplotlib.pyplot as plt

N = 100
t = 1

a1 = np.full((N-1,), -t)
a2 = np.full((N,), 2*t)
Hamiltonian = np.diag(a1, -1) +  np.diag(a2) + np.diag(a1, 1)

eval, evec = np.linalg.eig(Hamiltonian)
idx = eval.argsort()[::-1]
eval, evec = eval[idx], evec[:,idx]

wave2 = evec[2] / np.sum(abs(evec[2]))
prob2 = evec[2]**2 / np.sum(evec[2]**2)

_ = plt.plot(wave2)
_ = plt.plot(prob2)
plt.show()

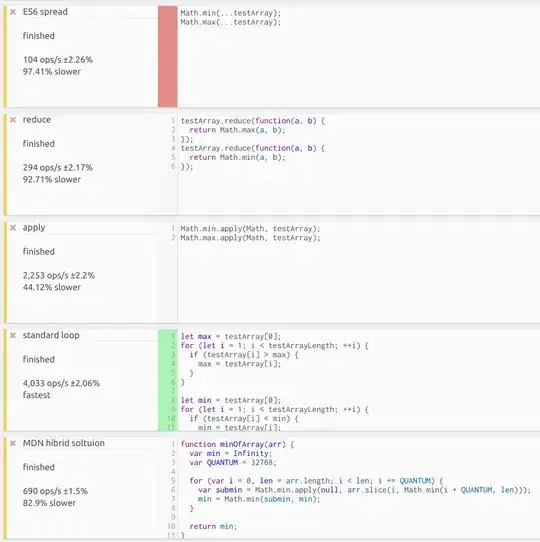
And the plot that comes out is this:

But I'd expect the blue line to be a sinoid as well. This has got me confused and I can't find what's causing the sudden sign changes. Plotting the function absolutely shows that the values associated with each x are fine, but the signs are screwed up.

Any ideas on what might cause this or how to solve it?

Can you tell why exactly you would expect to have all coordiantes of the third eigenvector to be positive? — ImportanceOfBeingErnest, Dec 06 '17 at 14:16
It is supposed to be a solution to the schrodinger equation. They shouldn't all be positive, but it should be described by a nice sineoid (i.e a wavefunction that solves the schrodinger equation). — Mitchell Faas, Dec 06 '17 at 14:18
Eigen vectors are not unique, there is no "shouldn't be all positive" because those are all still valid eigen vectors/values here. — Krupip, Dec 06 '17 at 14:22
Seems more like a physics question than one about programming. — ImportanceOfBeingErnest, Dec 06 '17 at 14:27
You use `evec[2]`, but the eigenvectors are in the *columns*, so it should be `evec[:,2]`. — Warren Weckesser, Dec 06 '17 at 14:27
Also note that you sorted the eigenvalues from highest to lowest. So the lowest frequency of oscillation will be the last column in `evec`. — Warren Weckesser, Dec 06 '17 at 14:51

score 4 · Accepted Answer · answered Dec 06 '17 at 15:03

Here's a modified version of your script that does what you expected. The changes are:

Corrected the indexing for the eigenvectors; they are the columns of evec.
Use np.linalg.eigh instead of np.linalg.eig. This isn't strictly necessary, but you might as well use the more efficient code.
Don't reverse the order of the sorted eigenvalues. I keep the eigenvalues sorted from lowest to highest. Because eigh returns the eigenvalues in ascending order, I just commented out the code that sorts the eigenvalues.

(Only the first change is a required correction.)

import numpy as np
import matplotlib
import matplotlib.pyplot as plt

N = 100
t = 1

a1 = np.full((N-1,), -t)
a2 = np.full((N,), 2*t)
Hamiltonian = np.diag(a1, -1) +  np.diag(a2) + np.diag(a1, 1)

eval, evec = np.linalg.eigh(Hamiltonian)
#idx = eval.argsort()[::-1]
#eval, evec = eval[idx], evec[:,idx]

k = 2
wave2 = evec[:, k] / np.sum(abs(evec[:, k]))
prob2 = evec[:, k]**2 / np.sum(evec[:, k]**2)

_ = plt.plot(wave2)
_ = plt.plot(prob2)
plt.show()

The plot:

If you take `k=-2`, corresponding to the case in the question where sorting is reversed you get again the oscillatory behaviour. So while this is all true from the computational point of view, the problem of the questioner is rather understanding the physics and accepting the fact that only is an observable quantity which should have the desired waveform, not v itself. — ImportanceOfBeingErnest, Dec 06 '17 at 15:28
Yes, the higher modes have higher frequencies. The *programming* problem here is simply the incorrect indexing of `evec`. — Warren Weckesser, Dec 06 '17 at 15:33

Krupip · Answer 2 · 2017-12-06T14:37:24.080

I may be wrong, but aren't they all valid eigen vectors/values? The sign shouldn't matter, as the definition of an eigen vector is:

In linear algebra, an eigenvector or characteristic vector of a linear transformation is a non-zero vector that only changes by an overall scale when that linear transformation is applied to it.

Just because the scale is negative doesn't mean it isn't valid.

See this post about Matlab's eig that has a similar problem

One way to fix this is to simply pick a sign for the start, and multiply everthing by -1 that doesn't fit that sign (or take abs of every element and multiply by your expected sign). For your results this should work (nothing crosses 0).

Neither matlab nor numpy care about what you are trying to solve, its simple mathematics that dictates that both signed eigenvector/value combinations are valid, your values are sinusoidal, its just that there exists two sets of eigenvector/values that work (negative and positive)

They are not, because they are solutions to the scrodinger equation which demands that the eigenvectors adhere to a function exp(ikx). So the eigenvalue must be a sinoid (at least the real part). — Mitchell Faas, Dec 06 '17 at 14:31
@MitchellFaas And eigen value/vector solvers don't care about the existence of Schrodingers equation, and your eigenvalues *ARE* sinusoidal, its just that because of this function in the definition of an eigenvector `A·v = λ·v` it also gives another valid eigen vector if your signs are flipped. — Krupip, Dec 06 '17 at 14:35

Eigen vectors in python giving seemingly random element-wise signs

2 Answers2