Shortest One-Way Path Through Multiple Nodes

Question

I have a series of graph coordinates and I need to find the shortest one-way path through them all. I have no predetermined start/end but each point must only be touched once and returning to the optimal origin is NOT required.

I've tried a couple TSP approaches, but they all seem to be based on returning to the origin at the end which gives terribly inefficient results in this case.

Example

1, 13
3, 0
3, 7
2, 21
2, 11
3, 12
1, 19
3, 6

would resolve to

3, 0
3, 6
3, 7
3, 12
2, 11
1, 13
1, 19
2, 21

Notes:

Yes I tried the search function, there is a basically identical question Algorithm: shortest path between all points however the only real answer is a TSP, which once again, closed circuit is inefficient for this.

It does not need to be 100% accurate, I already have a permutations method but its far too slow, I need to handle at least ~25-30 points, settling with a good approximation works for me

Thanks in advance.

Edit to clarify, TSP tends to solve as in img #1, my desired result is img #2
img 3 is the above sample solved via a TSP and img #4 is the desired (x coords shifted back -.5 for visibility)

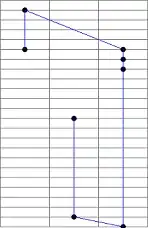
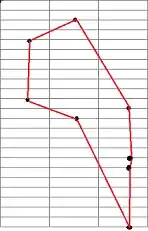
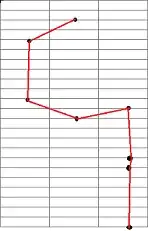
Couple more for good measure #1 = TSP, #2 = desired

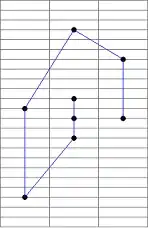
Basically i want the shortest chain connecting n points, using whichever start and end point is most efficient

Answer 1

This is an instance of the all-pairs shortest path problem with all edges having weight=1. You'll find common solutions like Dijkstra's or A-star algorithm on the linked page.
A naive approach is to iterate over the nodes and find the shortest path to every other node.

$paths = array();
foreach ($nodes as $start) {
    foreach ($nodes as $end) {
        if ($start !== $end) {
            $path[$start][$end] = findShortestPath($graph, $start, $end);
        }
    }
}

In a more sophisticated approach findShortestPath would remember subpaths of previous runs (or use $paths for that purpose) to gain better performance.

Answer 2

Since you don't care about finding a closed loop - all you need is a single path - you can make a small modification to the points you have to avoid the cost of a closed loop. To do this, add a new point, call it v, that you define to be at distance 0 from all the other points. Now, find a TSP solution for this graph. At some point, you'll enter and then leave v. If you take the cycle and then remove the edges into and out of v from it, then you'll have a path that visits each node exactly once without any cycles.

This still requires you to solve or approximate TSP, but it eliminates the huge overhead of returning to your start point.

Answer 3

there are many algorithms that search the shortest closed path in a graph. I think that it's not too hard to adapt one of the algorithms that solve that problem (a.k.a as travelling salesman problem) to your needs(the path should be a hamiltonian way not a hamiltonian cycle). Some of the well-known solutions for the salesman problem are Dijkstra's algorithm and Prim's algorithm.