I need to assign value to points in a 3D array that are inside an ellipsoid. The ellipsoid equation should be something like this:
r=b.sin(u)
x=r.cos(v)
y=r.sin(v)
z=a.cos(u).
But I think that this is only visual. I already tried something with a mask over a cubic array:
a, b = (size-1)/2, (size-1)/2
n = size
r = (size-1)/2
y,x = np.ogrid[-a:n-a, -b:n-b]
mask = x*x + y*y <= r*r # circle mask
array = np.zeros((n, n, n))
array[mask] = 10
But this creates a circle only in x and y which gives me:  /
/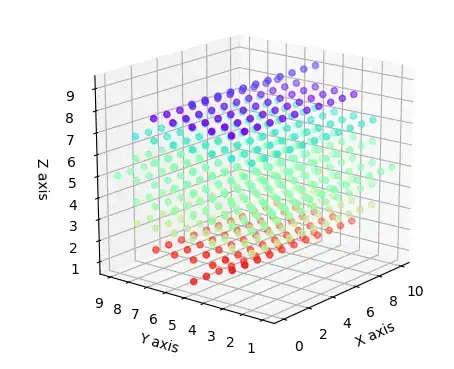 .
.
It's not a sphere. (and I need an ellipsoid).
Any ideas?