helix-shaped movement of an object in Matlab

Question

I have found this equation in a paper which represents a helix-shaped movement of an object:

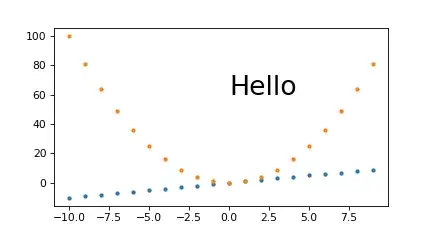
When I plotted the S vector in Matlab I got a different result, not helix shape.

Where is the problem, is it in the equation or in the code?

l is a random number in [-1,1]

r is a random vector in [0,1]

b is a constant for defining the shape of the logarithmic spiral.

Matlab code:

dim =3;
Max_iter =10;
X_star=zeros(1,dim);
ub = 100;
lb = -100;
X=rand(1,dim).*(ub-lb)+lb;
S = [];
t=0;
while t<Max_iter
    a=-1+t*((-1)/Max_iter);
    r=rand();   
    b=1;              
    l=(a-1)*rand + 1;   
     for j=1:size(X,2)
          D= abs(X_star(j) - X(1,j));    
          X(1,j)= D * exp(b.*l).* cos(l.*2*pi) + X_star(j);
     end
     X_star=X(1,:);

     S = [S X];
     plot(S); 

     t = t+1;
end

What does `C` do here? You assign a random value to it, but you never use it! Have you tried setting `l` at the beginning of your program, instead of changing it at every step? Or is this meant to be a helix-like random motion? — Cris Luengo, Jan 05 '18 at 06:31
What is `X_star` supposed to be? You set it to 0 and never change it. What is the source of this equation? There's information missing here. — Cris Luengo, Jan 05 '18 at 06:36
i feel like a helix-shaped movement has to happen in 3 dimensional space. i ran your code and S is a 1x30 vector. do you want the 3 X values to be coordinates? — Finn, Jan 05 '18 at 09:12

Spektre · Accepted Answer · 2018-01-05T09:21:26.417

0

that equations does not look like helix at all. Lets do this for 3D. First some definitions:

p0,p1 - centers of start and end of the helix 3D points
r - scalar radius of the helix
m - scalar number of screws (if not integer than the screws will not start and end at the same angular position)

We first need TBN vectors:

n = p1-p0
t = (1,0,0)
if (|dot(n/|n|,t)|>0.9) t = (0,1,0)
b = cross(n,t)
b = r*b / |b|
t = cross(b,n)
t = r*t / |t|

And now we can do the helix using TBN as basis vectors:

//                 x'                y'         z'
p(a) = p0 + t*cos(2*Pi*m*a) + b*sin(2*Pi*m*a) + n*a

Where a = <0.0,1.0> is the parameter which point on helix you want. If you move out of this interval you will extrapolate the helix before p0 and after p1. You can consider a is the time...

As you can see the equation is just 2D parametric circle (x',y') + linear movement (z') and transformed by basis vectors to p0,p1 direction and position.

If you need equations/code for the dot,cross and abs value of 3D vectors see:

Understanding 4x4 homogenous transform matrices

They are at the bottom of that answer of mine.

edited Jan 05 '18 at 09:21

answered Jan 05 '18 at 09:10

Spektre

49,595
11
110
380

thank you very much for your answer. Would you please check this paper "The Whale Optimization Algorithm" Section 2.2.2 , ***2 Spiral updating position***, I have found the equation there. The author mentioned that: _"A spiral equation is then created between the position of whale and prey to mimic the helix-shaped movement of humpback whales...."_ – Shdotcom Jan 05 '18 at 09:41
@Shdotcom I see no link in your comment – Spektre Jan 05 '18 at 09:45
@Shdotcom I find only [this](https://www.sciencedirect.com/science/article/pii/S0965997816300163) Which looks like it is not for free so I can not read the section you used. My bet is that the `X,X*,D',C` are some input vectors/tensors/parameters for some control equation/function that they use in the optimization process which is later on converted to the final position or speed/acceleration via **d'Lambert** And most likelly they are not in 3D Cartesian space at all. But that is just my gut feeling impression of it. – Spektre Jan 05 '18 at 10:10
X(t) is a the position vector at time _t_. The equation in the question is used to updated X(t). X_star is a best position obtained so far. So, the new position X(t+1) will be updated based on the X_star(t) using the equation mentioned in my question. The dimension of X is depend on the optimization problem, it can be 3D or 10D, 30 or nD. but in all case same equation has been used to update the positions. But I could not understand how the equation represents or mimic the ***helix-shaped movement*** – Shdotcom Jan 05 '18 at 11:15
That is why I want to plot X to see how does the movement look like. – Shdotcom Jan 05 '18 at 11:22
@Shdotcom `X-X*` is something like derivation which is analogy to velocity vector. The `cos` could turn it somehow mathematically to create helix shape but that is pure speculation from my side as I do not have any background knowledge or experience with the stuff. From geometrical point of view I see no helix there. – Spektre Jan 05 '18 at 12:14
I have another question, I have posted [here](https://math.stackexchange.com/questions/2592749/transform-n-sphere-hypersphere-to-x1-x2-x3-xn), would you please help me? – Shdotcom Jan 05 '18 at 12:26
@Shdotcom 1. see [Wiki: n-sphere spherical coordiantes](https://en.wikipedia.org/wiki/N-sphere) that should answer your other question. 2. Your helix has varying radius so you need to introduce also some function for `r` line `r(a) = r0*(1.0-a)` but that is linear to match the image you need to use another function possibly non linear like `r(a)=r0*(1.0-a)^q` where `q` is some constant try `0.5` or `2.0` ... From the paper I got a feeling that the optimization process turns that equation into system of differential equation like ODE but that is above my experience and more suited for math SE – Spektre Jan 05 '18 at 12:46
@Shdotcom also check if publishing that link to that paper does not violate some right as this is global site. In case it does delete that comment ... – Spektre Jan 05 '18 at 12:47

helix-shaped movement of an object in Matlab

1 Answers1