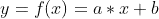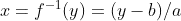First, it is better to use the def ... statement rather than lambda to define named functions. Have a look at this SO question and its answers for more details. But if I understand correctly what you want to achieve, it might be better to define the linear function as a class (see below).
The inverse of the linear function:
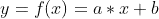
is given by:
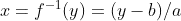
and depends on both the slope a and the intercept b. An important consequence of this is that you need to know both a and b to define its inverse in a functional form.
In python you can achieve this for example if you define a class of linear functions and the inverse as one of its methods:
class f_lin:
def __init__(self, a, b=0):
self.a = float(a)
self.b = b
def __call__(self, x):
return self.a * x + self.b
def inv(self, y):
return (y - self.b) / self.a
Now you can define:
inches_to_meters = f_lin(0.0254)
and use it like so:
inches_to_meters(10)
Out[38]: 0.254
inches_to_meters.inv(0.254)
Out[39]: 10.0
inches_to_meters.inv(inches_to_meters(10))
Out[40]: 10.0
Alternatively you could also create a new object for the inverse, as the inverse of a linear function is still a linear function:
class f_lin:
def __init__(self, a, b=0):
self.a = float(a)
self.b = b
def __call__(self, x):
return self.a * x + self.b
def get_inverse(self):
return self.__class__(1/self.a, - self.b/self.a)
Then you can define the inverse function like so:
inches_to_meters = f_lin(0.0254)
meters_to_inches = inches_to_meters.get_inverse()
Now you have both the linear function and its inverse as objects:
inches_to_meters(10)
Out[43]: 0.254
meters_to_inches(0.254)
Out[44]: 10.0
inches_to_meters(meters_to_inches(10))
Out[45]: 10.0
Those are just 2 ways of doing, both not using lambda as requested. However I would advise against doing such things with lambda.