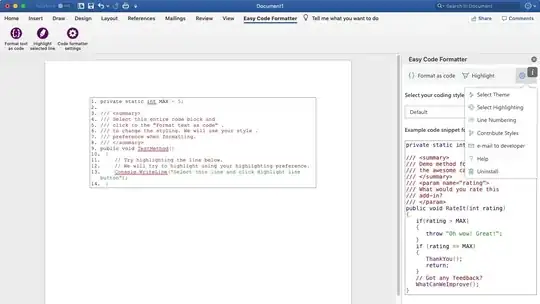
Suppose a Fibonacci algorithm:
We are asked to prove the upper/lower bound of this algorithm.
How do I proceed?
Update
So I'll explain what I have done myself and show where I'm stuck.
I don't know why but I decided to use recurrence relation here to see where I can get my final result. But the reason why I doubt my working out is that Upper/lower bound is the identification of the "limitless" of an algorithm in terms of resources.
So, the parallel algorithm has:
Work(n) = W(n - 1) + W(n - 2) + Θ(1)
At this point, I decided to use recurrence relation - have no idea -
Work(n) = [W(n - 1) + W(n - 2) + Θ(1)] + W(n - 2) + Θ(1)
= W(n - 2) + W(n - 2) + 2Θ(1)
= 2W(n - 2) + 2
= Stuck here
Honestly, I don't know even if that makes sense.
But I didn't quite understand the steps that were taken above