Blau index of Diversity in R

Question

I am trying to calculate the Blau index of diversity (gini-simpson) in R on my data frame. I have 6 columns for each person in a group, with values ranging from "Student", "Faculty", "Alumni" "Not Applicable". There are also NA's within the columns if a group is smaller than 6.

I would like to calculate the Blau index across the rows (the diversity across the entire group) not within each column, with na.rm= TRUE.

Does anyone know how to do this in R?

Thanks so much!

See here for a picture of data frame

Please provide your data as a reproducible example so that we can help you! https://stackoverflow.com/questions/5963269/how-to-make-a-great-r-reproducible-example — qdread, Jan 21 '18 at 22:18
There are some R packages that have builtin functions to calculate that index, including `diverse`. — qdread, Jan 21 '18 at 22:19

Maurits Evers · Accepted Answer · 2018-01-23T00:30:03.523

We can calculate the Gini-Simpson index quite easily by hand.

First off, I'll generate some sample data:

# Generate sample data
set.seed(2017);
type <- c("Student", "Faculty", "Alumni");
data <- sample(type, 6 * 20, replace = TRUE);

# Replace 40 entries with NAs
set.seed(2017);
data[sample(6 * 20, 40)] <- NA;

# Reformat as 6 column dataframe
df <- as.data.frame(matrix(data, ncol = 6), stringsAsFactors = FALSE);
names(df) <- paste0("e", seq(1:6), "_affiliation");
head(df);
#e1_affiliation e2_affiliation e3_affiliation e4_affiliation e5_affiliation
#1           <NA>        Faculty           <NA>        Student        Student
#2           <NA>           <NA>           <NA>        Faculty         Alumni
#3           <NA>         Alumni        Student        Faculty        Faculty
#4        Student           <NA>           <NA>           <NA>           <NA>
#5           <NA>        Student         Alumni         Alumni        Student
#6         Alumni         Alumni        Faculty        Faculty        Student
# e6_affiliation
#1         Alumni
#2         Alumni
#3           <NA>
#4        Student
#5        Faculty
#6        Student

The Gini-Simpson (= Gibbs-Martin = Blau) index of diversity is given by

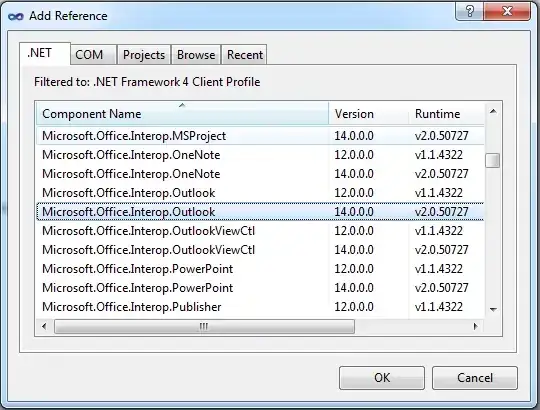
where R denotes the total number of types, and 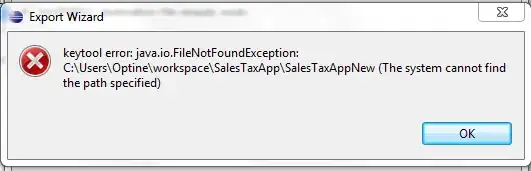is the proportional abundance of the ith type.

We define a function that takes a vector of strings and returns the GS index:

# Define function to calculate the Gini-Simpson index
# We ensure the same levels (present or absent) of x
# by factor(x, levels = type)
# Note that NAs will not be considered by default
get.GS.index <- function(x, type) {
    x <- factor(x, levels = type);
    return(1 - sum(prop.table(table(x))^2));
}

We can now apply get.GS.index to all rows of the dataframe

apply(df, 1, get.GS.index, type)
#[1] 0.6250000 0.4444444 0.6250000 0.0000000 0.6400000 0.6666667 0.5000000
#[8] 0.6250000 0.6400000 0.5000000 0.4444444 0.6400000 0.3750000 0.3750000
#[15] 0.0000000 0.0000000 0.6111111 0.4444444 0.6666667 0.6400000

Update

We can modify the function get.GS.index to return NA if there is only one type present in a group.

get.GS.index <- function(x, type) {
    x <- factor(x, levels = type);
    t <- table(x);
    if (length(t[t>0]) == 1) return(NA) else return(1 - sum(prop.table(t)^2));
}

apply(df, 1, get.GS.index, type);
# [1] 0.6250000 0.4444444 0.6250000        NA 0.6400000 0.6666667 0.5000000
# [8] 0.6250000 0.6400000 0.5000000 0.4444444 0.6400000 0.3750000 0.3750000
#[15]        NA        NA 0.6111111 0.4444444 0.6666667 0.6400000

No worries @PascaleFricke, glad to help. If this answers your question please consider closing the question by accepting & upvoting the answer. — Maurits Evers, Jan 22 '18 at 01:20
Hi Mauritz. Just one more question. I would only like to calculate the Blau for groups with more than one person (If there is only one entrepreneur a diversity measure doesn't really make sense). I have another column with number of entrepreneurs, and am trying to incorporate an If statement (If number of entrepreneurs is >1, then I would like the Blau but if there is only 1, I would like NA). I'm not sure how to do this. Do you have an idea of how to embed this into the function previously defined? Thanks! — Pascale Fricke, Jan 22 '18 at 20:57
@PascaleFricke I suggest you accept & upvote this answer first so that we can close it; I'll edit my solution to return NAs when there's only one type present in a group. — Maurits Evers, Jan 22 '18 at 22:07
@PascaleFricke I've edited my answer to account for groups with a single type as per your request. — Maurits Evers, Jan 23 '18 at 00:31

Blau index of Diversity in R

1 Answers1

Update