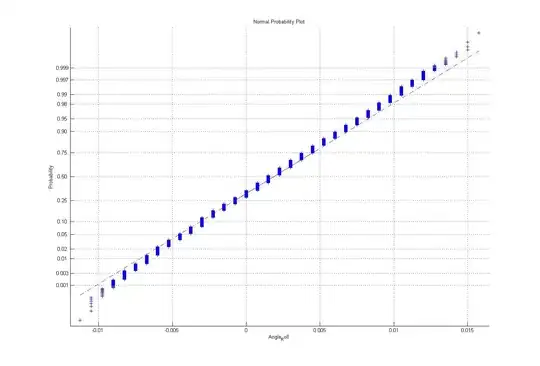
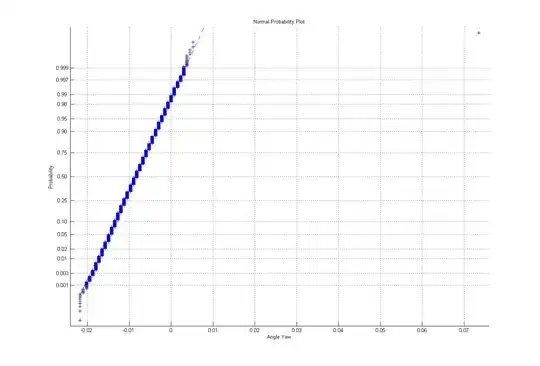
I have a very basic question. What is the basis of the normal probability plot i.e. what do the probabilities represent? I am testing for a standard normal distribution. My normplot (in MATLAB) revealed that the values were more or less in a straight line BUT the probability of 0.5 corresponded to a value other than zero.
My question is, how do I interpret this? Does this mean that my data is normally distributed but has a non-zero mean (i.e. not standard normal) or does this probability only reflect something else? I tried Google and one link said the probabilities are the cumulative probabilities from the z-table, and I can't figure out what to make of it.
Also in MATLAB, is it that as long as the values are fitting into the line drawn by the program (the red dotted line) the values come from a normal distribution? In one of my graphs, the dotted line is very steep but the values fit in, does this mean that the one or two values that are way outside this line are just outliers?
I'm very new to stats, so please help!
Thanks!