I found out that it is possible to fit a gaussian mixture model to a 1-dimensional signal with sklearn (e.g. a histogram, see fist image) with sklearn.mixture.GaussianMixture (see here)
I now would like to fit a gaussian mixture model in 2 dimensions (e.g. see second image). Is that possible too?
You can apply the same approach. First make model fit the data (Now it has 2 columns representing x and y values). Then calculate the likelihood of any point you want.
In the example below, points are generated from 2 gaussian distribution.
# Generate Data
data1 = np.random.multivariate_normal( [3,3], [[1, 0], [0, 1]], 80)
data2 = np.random.multivariate_normal( [-4,2], [[1, 1.5], [1.5, 3]], 120)
X = np.concatenate((data1, data2))
plt.axis([-8, 8, -8, 8])
plt.scatter(X.T[0], X.T[1])
plt.show()
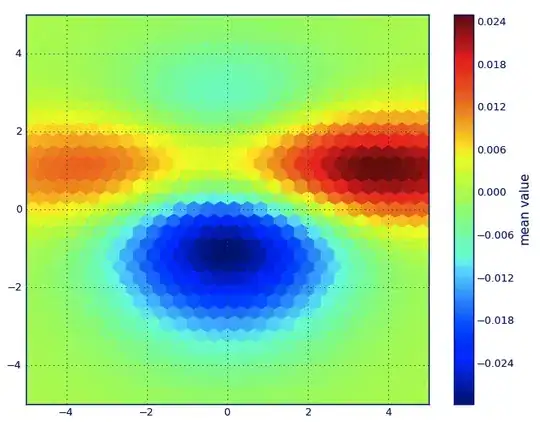
Then fit the data. Note that you should know the number of distribution (in this case it is 2).
# Fit the data
gmm = GaussianMixture(n_components=2)
gmm.fit(X)
Now, you have estimated parameters of distributions. You can calculate the probability of any point by using them.
# Distribution parameters
print(gmm.means_)
[[-3.87809034 2.15419139]
[ 3.07939341 3.02521961]]
print(gmm.covariances_)
[[[ 0.78359622 1.11780271]
[ 1.11780271 2.31658265]]
[[ 0.80263971 -0.03346032]
[-0.03346032 1.04663585]]]
or score_sample method can be used instead. This method returns log likelihood of given points.
lin_param = (-8, 8, 100)
x = np.linspace(*lin_param)
y = np.linspace(*lin_param)
xx, yy = np.meshgrid(x, y)
pos = np.concatenate((xx.reshape(-1, 1), yy.reshape(-1, 1)), axis = 1)
z = gmm.score_samples(pos) # Note that this method returns log-likehood
# z = np.exp(gmm.score_samples(pos)) # e^x to get likehood values
z = z.reshape(xx.shape)
plt.contourf(x, y, z, 50, cmap="viridis")
plt.show()
