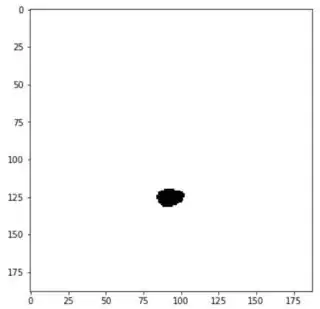
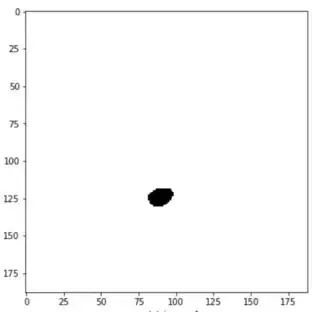
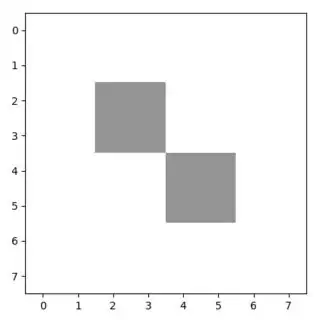
I'm trying to interpolate between two images in Python.
Images are of shapes (188, 188)
I wish to interpolate the image 'in-between' these two images. Say Image_1 is at location z=0 and Image_2 is at location z=2. I want the interpolated image at location z=1.
I believe this answer (MATLAB) contains a similar problem and solution.
Creating intermediate slices in a 3D MRI volume with MATLAB
I've tried to convert this code to Python as follows:
from scipy.interpolate import interpn
from scipy.interpolate import griddata
# Construct 3D volume from images
# arr.shape = (2, 182, 182)
arr = np.r_['0,3', image_1, image_2]
slices,rows,cols = arr.shape
# Construct meshgrids
[X,Y,Z] = np.meshgrid(np.arange(cols), np.arange(rows), np.arange(slices));
[X2,Y2,Z2] = np.meshgrid(np.arange(cols), np.arange(rows), np.arange(slices*2));
# Run n-dim interpolation
Vi = interpn([X,Y,Z], arr, np.array([X1,Y1,Z1]).T)
However, this produces an error:
ValueError: The points in dimension 0 must be strictly ascending
I suspect I am not constructing my meshgrid(s) properly but am kind of lost on whether or not this approach is correct.
Any ideas?
---------- Edit -----------
Found some MATLAB code that appears to solve this problem:
Interpolating Between Two Planes in 3d space
I attempted to convert this to Python:
from scipy.ndimage.morphology import distance_transform_edt
from scipy.interpolate import interpn
def ndgrid(*args,**kwargs):
"""
Same as calling ``meshgrid`` with *indexing* = ``'ij'`` (see
``meshgrid`` for documentation).
"""
kwargs['indexing'] = 'ij'
return np.meshgrid(*args,**kwargs)
def bwperim(bw, n=4):
"""
perim = bwperim(bw, n=4)
Find the perimeter of objects in binary images.
A pixel is part of an object perimeter if its value is one and there
is at least one zero-valued pixel in its neighborhood.
By default the neighborhood of a pixel is 4 nearest pixels, but
if `n` is set to 8 the 8 nearest pixels will be considered.
Parameters
----------
bw : A black-and-white image
n : Connectivity. Must be 4 or 8 (default: 8)
Returns
-------
perim : A boolean image
From Mahotas: http://nullege.com/codes/search/mahotas.bwperim
"""
if n not in (4,8):
raise ValueError('mahotas.bwperim: n must be 4 or 8')
rows,cols = bw.shape
# Translate image by one pixel in all directions
north = np.zeros((rows,cols))
south = np.zeros((rows,cols))
west = np.zeros((rows,cols))
east = np.zeros((rows,cols))
north[:-1,:] = bw[1:,:]
south[1:,:] = bw[:-1,:]
west[:,:-1] = bw[:,1:]
east[:,1:] = bw[:,:-1]
idx = (north == bw) & \
(south == bw) & \
(west == bw) & \
(east == bw)
if n == 8:
north_east = np.zeros((rows, cols))
north_west = np.zeros((rows, cols))
south_east = np.zeros((rows, cols))
south_west = np.zeros((rows, cols))
north_east[:-1, 1:] = bw[1:, :-1]
north_west[:-1, :-1] = bw[1:, 1:]
south_east[1:, 1:] = bw[:-1, :-1]
south_west[1:, :-1] = bw[:-1, 1:]
idx &= (north_east == bw) & \
(south_east == bw) & \
(south_west == bw) & \
(north_west == bw)
return ~idx * bw
def signed_bwdist(im):
'''
Find perim and return masked image (signed/reversed)
'''
im = -bwdist(bwperim(im))*np.logical_not(im) + bwdist(bwperim(im))*im
return im
def bwdist(im):
'''
Find distance map of image
'''
dist_im = distance_transform_edt(1-im)
return dist_im
def interp_shape(top, bottom, num):
if num<0 and round(num) == num:
print("Error: number of slices to be interpolated must be integer>0")
top = signed_bwdist(top)
bottom = signed_bwdist(bottom)
r, c = top.shape
t = num+2
print("Rows - Cols - Slices")
print(r, c, t)
print("")
# rejoin top, bottom into a single array of shape (2, r, c)
# MATLAB: cat(3,bottom,top)
top_and_bottom = np.r_['0,3', top, bottom]
#top_and_bottom = np.rollaxis(top_and_bottom, 0, 3)
# create ndgrids
x,y,z = np.mgrid[0:r, 0:c, 0:t-1] # existing data
x1,y1,z1 = np.mgrid[0:r, 0:c, 0:t] # including new slice
print("Shape x y z:", x.shape, y.shape, z.shape)
print("Shape x1 y1 z1:", x1.shape, y1.shape, z1.shape)
print(top_and_bottom.shape, len(x), len(y), len(z))
# Do interpolation
out = interpn((x,y,z), top_and_bottom, (x1,y1,z1))
# MATLAB: out = out(:,:,2:end-1)>=0;
array_lim = out[-1]-1
out[out[:,:,2:out] >= 0] = 1
return out
I call this as follows:
new_image = interp_shape(image_1,image_2, 1)
Im pretty sure this is 80% of the way there but I still get this error when running:
ValueError: The points in dimension 0 must be strictly ascending
Again, I am probably not constructing my meshes correctly. I believe np.mgrid should produce the same result as MATLABs ndgrid though.
Is there a better way to construct the ndgrid equivalents?