Question:
I've profiled my Python program to death, and there is one function that is slowing everything down. It uses Python dictionaries heavily, so I may not have used them in the best way. If I can't get it running faster, I will have to re-write it in C++, so is there anyone who can help me optimise it in Python?
I hope I've given the right sort of explanation, and that you can make some sense of my code! Thanks in advance for any help.
My code:
This is the offending function, profiled using line_profiler and kernprof. I'm running Python 2.7
I'm particularly puzzled by things like lines 363, 389 and 405, where an if statement with a comparison of two variables seems to take an inordinate amount of time.
I've considered using NumPy (as it does sparse matrices) but I don't think it's appropriate because: (1) I'm not indexing my matrix using integers (I'm using object instances); and (2) I'm not storing simple data types in the matrix (I'm storing tuples of a float and an object instance). But I'm willing to be persuaded about NumPy. If anyone knows about NumPy's sparse matrix performance vs. Python's hash tables, I'd be interested.
Sorry I haven't given a simple example that you can run, but this function is tied up in a much larger project and I couldn't work out how to set up a simple example to test it, without giving you half of my code base!
Timer unit: 3.33366e-10 s
File: routing_distances.py
Function: propagate_distances_node at line 328
Total time: 807.234 s
Line # Hits Time Per Hit % Time Line Contents
328 @profile
329 def propagate_distances_node(self, node_a, cutoff_distance=200):
330
331 # a makes sure its immediate neighbours are correctly in its distance table
332 # because its immediate neighbours may change as binds/folding change
333 737753 3733642341 5060.8 0.2 for (node_b, neighbour_distance_b_a) in self.neighbours[node_a].iteritems():
334 512120 2077788924 4057.2 0.1 use_neighbour_link = False
335
336 512120 2465798454 4814.9 0.1 if(node_b not in self.node_distances[node_a]): # a doesn't know distance to b
337 15857 66075687 4167.0 0.0 use_neighbour_link = True
338 else: # a does know distance to b
339 496263 2390534838 4817.1 0.1 (node_distance_b_a, next_node) = self.node_distances[node_a][node_b]
340 496263 2058112872 4147.2 0.1 if(node_distance_b_a > neighbour_distance_b_a): # neighbour distance is shorter
341 81 331794 4096.2 0.0 use_neighbour_link = True
342 496182 2665644192 5372.3 0.1 elif((None == next_node) and (float('+inf') == neighbour_distance_b_a)): # direct route that has just broken
343 75 313623 4181.6 0.0 use_neighbour_link = True
344
345 512120 1992514932 3890.7 0.1 if(use_neighbour_link):
346 16013 78149007 4880.3 0.0 self.node_distances[node_a][node_b] = (neighbour_distance_b_a, None)
347 16013 83489949 5213.9 0.0 self.nodes_changed.add(node_a)
348
349 ## Affinity distances update
350 16013 86020794 5371.9 0.0 if((node_a.type == Atom.BINDING_SITE) and (node_b.type == Atom.BINDING_SITE)):
351 164 3950487 24088.3 0.0 self.add_affinityDistance(node_a, node_b, self.chemistry.affinity(node_a.data, node_b.data))
352
353 # a sends its table to all its immediate neighbours
354 737753 3549685140 4811.5 0.1 for (node_b, neighbour_distance_b_a) in self.neighbours[node_a].iteritems():
355 512120 2129343210 4157.9 0.1 node_b_changed = False
356
357 # b integrates a's distance table with its own
358 512120 2203821081 4303.3 0.1 node_b_chemical = node_b.chemical
359 512120 2409257898 4704.5 0.1 node_b_distances = node_b_chemical.node_distances[node_b]
360
361 # For all b's routes (to c) that go to a first, update their distances
362 41756882 183992040153 4406.3 7.6 for node_c, (distance_b_c, node_after_b) in node_b_distances.iteritems(): # Think it's ok to modify items while iterating over them (just not insert/delete) (seems to work ok)
363 41244762 172425596985 4180.5 7.1 if(node_after_b == node_a):
364
365 16673654 64255631616 3853.7 2.7 try:
366 16673654 88781802534 5324.7 3.7 distance_b_a_c = neighbour_distance_b_a + self.node_distances[node_a][node_c][0]
367 187083 929898684 4970.5 0.0 except KeyError:
368 187083 1056787479 5648.8 0.0 distance_b_a_c = float('+inf')
369
370 16673654 69374705256 4160.7 2.9 if(distance_b_c != distance_b_a_c): # a's distance to c has changed
371 710083 3136751361 4417.4 0.1 node_b_distances[node_c] = (distance_b_a_c, node_a)
372 710083 2848845276 4012.0 0.1 node_b_changed = True
373
374 ## Affinity distances update
375 710083 3484577241 4907.3 0.1 if((node_b.type == Atom.BINDING_SITE) and (node_c.type == Atom.BINDING_SITE)):
376 99592 1591029009 15975.5 0.1 node_b_chemical.add_affinityDistance(node_b, node_c, self.chemistry.affinity(node_b.data, node_c.data))
377
378 # If distance got longer, then ask b's neighbours to update
379 ## TODO: document this!
380 16673654 70998570837 4258.1 2.9 if(distance_b_a_c > distance_b_c):
381 #for (node, neighbour_distance) in node_b_chemical.neighbours[node_b].iteritems():
382 1702852 7413182064 4353.4 0.3 for node in node_b_chemical.neighbours[node_b]:
383 1204903 5912053272 4906.7 0.2 node.chemical.nodes_changed.add(node)
384
385 # Look for routes from a to c that are quicker than ones b knows already
386 42076729 184216680432 4378.1 7.6 for node_c, (distance_a_c, node_after_a) in self.node_distances[node_a].iteritems():
387
388 41564609 171150289218 4117.7 7.1 node_b_update = False
389 41564609 172040284089 4139.1 7.1 if(node_c == node_b): # a-b path
390 512120 2040112548 3983.7 0.1 pass
391 41052489 169406668962 4126.6 7.0 elif(node_after_a == node_b): # a-b-a-b path
392 16251407 63918804600 3933.1 2.6 pass
393 24801082 101577038778 4095.7 4.2 elif(node_c in node_b_distances): # b can already get to c
394 24004846 103404357180 4307.6 4.3 (distance_b_c, node_after_b) = node_b_distances[node_c]
395 24004846 102717271836 4279.0 4.2 if(node_after_b != node_a): # b doesn't already go to a first
396 7518275 31858204500 4237.4 1.3 distance_b_a_c = neighbour_distance_b_a + distance_a_c
397 7518275 33470022717 4451.8 1.4 if(distance_b_a_c < distance_b_c): # quicker to go via a
398 225357 956440656 4244.1 0.0 node_b_update = True
399 else: # b can't already get to c
400 796236 3415455549 4289.5 0.1 distance_b_a_c = neighbour_distance_b_a + distance_a_c
401 796236 3412145520 4285.3 0.1 if(distance_b_a_c < cutoff_distance): # not too for to go
402 593352 2514800052 4238.3 0.1 node_b_update = True
403
404 ## Affinity distances update
405 41564609 164585250189 3959.7 6.8 if node_b_update:
406 818709 3933555120 4804.6 0.2 node_b_distances[node_c] = (distance_b_a_c, node_a)
407 818709 4151464335 5070.7 0.2 if((node_b.type == Atom.BINDING_SITE) and (node_c.type == Atom.BINDING_SITE)):
408 104293 1704446289 16342.9 0.1 node_b_chemical.add_affinityDistance(node_b, node_c, self.chemistry.affinity(node_b.data, node_c.data))
409 818709 3557529531 4345.3 0.1 node_b_changed = True
410
411 # If any of node b's rows have exceeded the cutoff distance, then remove them
412 42350234 197075504439 4653.5 8.1 for node_c, (distance_b_c, node_after_b) in node_b_distances.items(): # Can't use iteritems() here, as deleting from the dictionary
413 41838114 180297579789 4309.4 7.4 if(distance_b_c > cutoff_distance):
414 206296 894881754 4337.9 0.0 del node_b_distances[node_c]
415 206296 860508045 4171.2 0.0 node_b_changed = True
416
417 ## Affinity distances update
418 206296 4698692217 22776.5 0.2 node_b_chemical.del_affinityDistance(node_b, node_c)
419
420 # If we've modified node_b's distance table, tell its chemical to update accordingly
421 512120 2130466347 4160.1 0.1 if(node_b_changed):
422 217858 1201064454 5513.1 0.0 node_b_chemical.nodes_changed.add(node_b)
423
424 # Remove any neighbours that have infinite distance (have just unbound)
425 ## TODO: not sure what difference it makes to do this here rather than above (after updating self.node_distances for neighbours)
426 ## but doing it above seems to break the walker's movement
427 737753 3830386968 5192.0 0.2 for (node_b, neighbour_distance_b_a) in self.neighbours[node_a].items(): # Can't use iteritems() here, as deleting from the dictionary
428 512120 2249770068 4393.1 0.1 if(neighbour_distance_b_a > cutoff_distance):
429 150 747747 4985.0 0.0 del self.neighbours[node_a][node_b]
430
431 ## Affinity distances update
432 150 2148813 14325.4 0.0 self.del_affinityDistance(node_a, node_b)
Explanation of my code:
This function maintains a sparse distance matrix representing the network distance (sum of edge weights on the shortest path) between nodes in a (very big) network. To work with the complete table and use the Floyd-Warshall algorithm would be very slow. (I tried this first, and it was orders of magnitude slower than the current version.) So my code uses a sparse matrix to represent a thresholded version of the full distance matrix (any paths with a distance greater than 200 units are ignored). The network topolgy changes over time, so this distance matrix needs updating over time. To do this, I am using a rough implementation of a distance-vector routing protocol: each node in the network knows the distance to each other node and the next node on the path. When a topology change happens, the node(s) associated with this change update their distance table(s) accordingly, and tell their immediate neighbours. The information spreads through the network by nodes sending their distance tables to their neighbours, who update their distance tables and spread them to their neighbours.
There is an object representing the distance matrix: self.node_distances. This is a dictionary mapping nodes to routing tables. A node is an object that I've defined. A routing table is a dictionary mapping nodes to tuples of (distance, next_node). Distance is the graph distance from node_a to node_b, and next_node is the neighbour of node_a that you must go to first, on the path between node_a and node_b. A next_node of None indicates that node_a and node_b are graph neighbours. For example, a sample of a distance matrix could be:
self.node_distances = { node_1 : { node_2 : (2.0, None),
node_3 : (5.7, node_2),
node_5 : (22.9, node_2) },
node_2 : { node_1 : (2.0, None),
node_3 : (3.7, None),
node_5 : (20.9, node_7)},
...etc...
Because of topology changes, two nodes that were far apart (or not connected at all) can become close. When this happens, entries are added to this matrix. Because of the thresholding, two nodes can become too far apart to care about. When this happens, entries are deleted from this matrix.
The self.neighbours matrix is similar to self.node_distances, but contains information about the direct links (edges) in the network. self.neighbours is continually being modified externally to this function, by the chemical reaction. This is where the network topology changes come from.
The actual function that I'm having problems with: propagate_distances_node() performs one step of the distance-vector routing protocol. Given a node, node_a, the function makes sure that node_a's neighbours are correctly in the distance matrix (topology changes). The function then sends node_a's routing table to all of node_a's immediate neighbours in the network. It integrates node_a's routing table with each neighbour's own routing table.
In the rest of my program, the propagate_distances_node() function is called repeatedly, until the distance matrix converges. A set, self.nodes_changed, is maintained, of the nodes that have changed their routing table since they were last updated. On every iteration of my algorithm, a random subset of these nodes are chosen and propagate_distances_node() is called on them. This means the nodes spread their routing tables asynchronously and stochastically. This algorithm converges on the true distance matrix when the set self.nodes_changed becomes empty.
The "affinity distances" parts (add_affinityDistance and del_affinityDistance) are a cache of a (small) sub-matrix of the distance matrix, that is used by a different part of the program.
The reason I'm doing this is that I'm simulating computational analogues of chemicals participating in reactions, as part of my PhD. A "chemical" is a graph of "atoms" (nodes in the graph). Two chemicals binding together is simulated as their two graphs being joined by new edges. A chemical reaction happens (by a complicated process that isn't relevant here), changing the topology of the graph. But what happens in the reaction depends on how far apart the different atoms are that make up the chemicals. So for each atom in the simulation, I want to know which other atoms it is close to. A sparse, thresholded distance matrix is the most efficient way to store this information. Since the topology of the network changes as the reaction happens, I need to update the matrix. A distance-vector routing protocol is the fastest way I could come up with of doing this. I don't need a more compliacted routing protocol, because things like routing loops don't happen in my particular application (because of how my chemicals are structured). The reason I'm doing it stochastically is so that I can interleve the chemical reaction processes with the distance spreading, and simulate a chemical gradually changing shape over time as the reaction happens (rather than changing shape instantly).
The self in this function is an object representing a chemical. The nodes in self.node_distances.keys() are the atoms that make up the chemical. The nodes in self.node_distances[node_x].keys() are nodes from the chemical and potentially nodes from any chemicals that the chemical is bound to (and reacting with).
Update:
I tried replacing every instance of node_x == node_y with node_x is node_y (as per @Sven Marnach's comment), but it slowed things down! (I wasn't expecting that!)
My original profile took 807.234s to run, but with this modification it increased to 895.895s. Sorry, I was doing the profiling wrong! I was using line_by_line, which (on my code) had far too much variance (that difference of ~90 seconds was all in the noise). When profiling it properly, is is detinitely faster than ==. Using CProfile, my code with == took 34.394s, but with is, it took 33.535s (which I can confirm is out of the noise).
Update: Existing libraries
I'm unsure as to whether there will be an existing library that can do what I want, since my requirements are unusual: I need to compute the shortest-path lengths between all pairs of nodes in a weighted, undirected graph. I only care about path lengths that are lower than a threshold value. After computing the path lengths, I make a small change to the network topology (adding or removing an edge), and then I want to re-compute the path lengths. My graphs are huge compared to the threshold value (from a given node, most of the graph is further away than the threshold), and so the topology changes don't affect most of the shortest-path lengths. This is why I am using the routing algorithm: because this spreads topology-change information through the graph structure, so I can stop spreading it when it's gone further than the threshold. i.e., I don't need to re-compute all the paths each time. I can use the previous path information (from before the topology change) to speed up the calculation. This is why I think my algorithm will be faster than any library implementations of shortest-path algorithms. I've never seen routing algorithms used outside of actually routing packets through physical networks (but if anyone has, then I'd be interested).
NetworkX was suggested by @Thomas K. It has lots of algorithms for calculating shortest paths. It has an algorithm for computing the all-pairs shortest path lengths with a cutoff (which is what I want), but it only works on unweighted graphs (mine are weighted). Unfortunately, its algorithms for weighted graphs don't allow the use of a cutoff (which might make them slow for my graphs). And none of its algorithms appear to support the use of pre-calculated paths on a very similar network (i.e. the routing stuff).
igraph is another graph library that I know of, but looking at its documentation, I can't find anything about shortest-paths. But I might have missed it - its documentation doesn't seem very comprehensive.
NumPy might be possible, thanks to @9000's comment. I can store my sparse matrix in a NumPy array if I assign a unique integer to each instance of my nodes. I can then index a NumPy array with integers instead of node instances. I will also need two NumPy arrays: one for the distances and one for the "next_node" references. This might be faster than using Python dictionaries (I don't know yet).
Does anyone know of any other libraries that might be useful?
Update: Memory usage
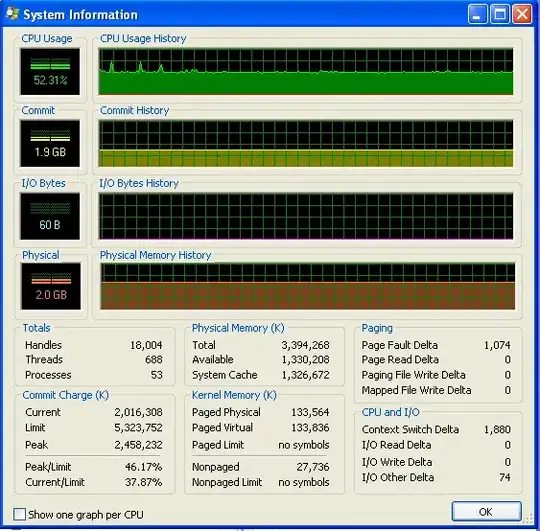
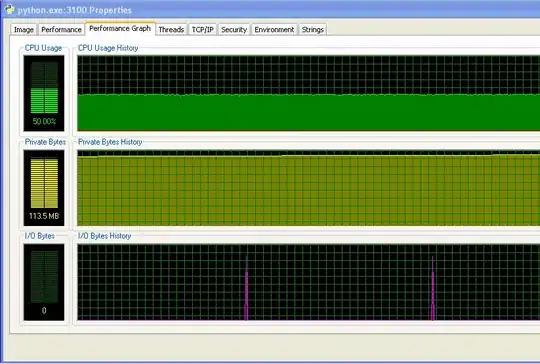
I'm running Windows (XP), so here is some info about memory usage, from Process Explorer. The CPU usage is at 50% because I have a dual-core machine.
My program doesn't run out of RAM and start hitting the swap. You can see that from the numbers, and from the IO graph not having any activity. The spikes on the IO graph are where the program prints to the screen to say how it's doing.
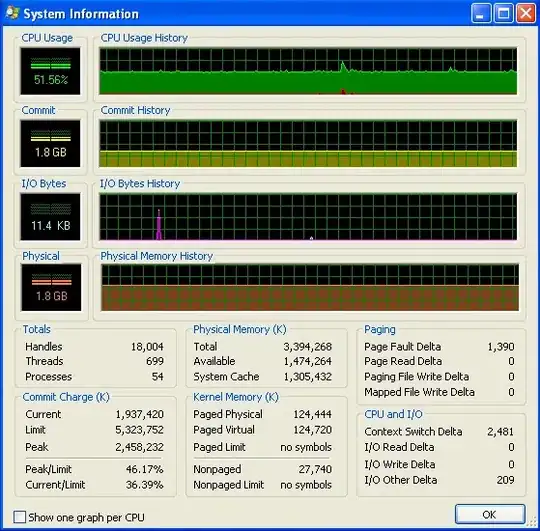
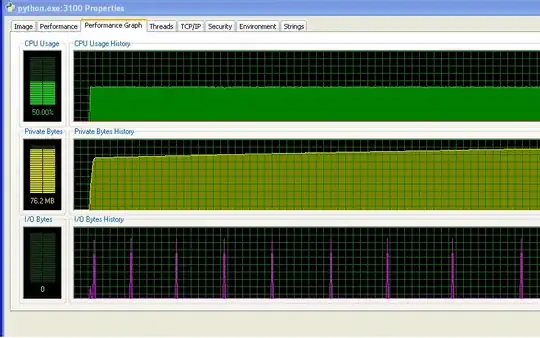
However, my program does keep using up more and more RAM over time, which is probably not a good thing (but it's not using up much RAM overall, which is why I didn't notice the increase until now).
And the distance between the spikes on the IO graph increases over time. This is bad - my program prints to the screen every 100,000 iterations, so that means that each iteration is taking longer to execute as time goes on... I've confirmed this by doing a long run of my program and measuring the time between print statements (the time between each 10,000 iterations of the program). This should be constant, but as you can see from the graph, it increases linearly... so something's up there. (The noise on this graph is because my program uses lots of random numbers, so the time for each iteration varies.)
After my program's been running for a long time, the memory usage looks like this (so it's definitely not running out of RAM):