Is calculating the index in an array more efficient than letting the compiler do it?

Question

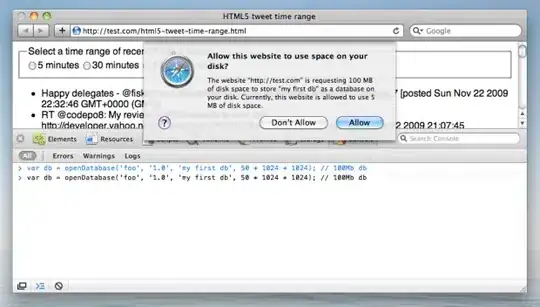
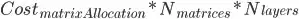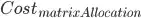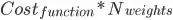I'm trying to generalize a neural network function to arbitrarily many layers, and so I need multiple matrices to hold the weights for each neuron in each layer. I was originally explicitly declaring matrix objects in R to hold my weights for each layer. Instead of having one matrix per layer, I thought of a way (not saying it's original), to store all of my weights in a single array and defined an "indexing function" to map a weight to its appropriate index in the array.

I defined the function as follows:

where is the k-th weight of the j-th neuron in the i-th layer and L(r) is the number of neurons in layer r. After writing these definitions, I realize that stackoverflow doesn't allow latex like mathoverflow which is unfortunate. Now the question is: Is it more efficient to compute the index of my weights in this way, or is actually less efficient? After looking up how indices are computed for arrays in general, this is essentially what is done on compilation anyway if I just kept a matrix in each layer holding the weights, so it seems like I may just be making my code overly complicated and harder to understand if there's no difference in time efficiency.

Answer 1

TL;DR use the matrices its easier to understand and takes advantage of optimized CPU instructions.

---

In computer science parlance, the efficiency (scalability) of algorithms is reasoned about using Big O cost. A score can be given to both the time and space complexity.
Using Big O notation lets compare the two approaches:

Array Approach

time complexity:
Array index access is O(1) time, no matter how large an array becomes, it is just as computationally easy to access an element given its index.

As you've created a function to compute the index of the k-th weight, this adds some small complexity but would probably run in constant O(1) time as it is a mathematical expression, so negligible.

space complexity: O(N) where N is the number of weights across all layers.

Matrices Approach

time complexity:
A matrix is essentially a 2d array with O(1) access

space complexity
O(N + M), where N is number of neurons and M is number of weights.

---

Conceptually, we can see that the two approaches have an equivalent time and space complexity score.
However there are the other trade-offs involved (and as a good SO-er must inform you of those)

When it comes to working with the data in the array vs matrices approach, the array approach is less efficient as it circumvents the opportunity for MISD operations. As @liborm alluded to there are vectorised (MISD) operations handled by lower level system libraries like LAPACK/BLAS, which "batch" CPU instructions for some matrix operations (less overhead cost to transfer and compute data at CPU compared to sending a new instruction every time)

Instead of having one matrix per layer, I thought of a way ... to store all of my weights in a single array

It's hard to see why you would opt-ed for the latter as it requires you to create a bespoke indexing function. Maybe its nicer to think about all your weights being in one long array place? However I would argue the mental load required to maintain the array mapping is higher than having multiple matrices dedicated to a layer.

A hash-table like structure of matrices would be much easier to reason about

layers <- list(layer1 = [[...]], layer2 = [[...]], layerN = [[...]])

Further reading

http://www.noamross.net/blog/2014/4/16/vectorization-in-r--why.html

Answer 2

There are many factors to take into consideration in each of the approaches. I'm not familiar with R but I'm assuming matrices' buffers are represented as one-dimensional arrays in memory. (Even if they are written as two dimensional arrays in the underlying C implementation the compiler stores it as one-dimensional array in memory)

The overall outline of memory operations are:

1. Case: Several matrices per layers

   • Allocation of matrices:
   • Accessing of indices:

2. Case: One matrix for all layers + index calculation

   • Allocation of matrix cost:
   • Accesing each of the indices cost:
   • Function cost:

We can clearly see that the second case, scales better, even though there's the additional cost of the function call.

Having said that, in general having a statically allocated array with all the weights for all the layers, should be faster.

In most cases, computers's bottleneck is memory bandwidth, and the best way to counteract this is to minimize the number of memory accesses.

With this in mind there's another more primitive reason why the 2nd approach will probably be faster: Caches.

Here's a good explanation of the performance difference in accesing a two-dimensional array in a loop by Good Ol' Bob Martin

TL; DR: Caches take advantage of the principle of locality, and therefore, having memory accesses spatially close to each other (as you would in one single array and accessing them in a cache-friendly way as explained in Bob Martin's answer) renders better performance than having them spatially separated (having them in several distinct arrays).

PS: I also recommend to benchmark both approaches and compare, since these nuances regarding the cache are machine-dependent. It might be the case that the Dataset/NN is small enough to fit completely in RAM or even in cache? in a very powerful server.

Answer 3

I'm sure you want to use some kind of native array objects, so you get the speedups provided by BLAS/LAPACK implementations (see eg Intel MKL discussion here if you're on Windows). Most of the time in NN evaluation will be spent in matrix multiplications (like SGEMM), and this is where BLAS implementations like Intel MKL can be an order of magnitude faster.

That is - even if the hand-coded indices for your single-array multi-layer network were super fast, you won't be able to use it with the optimised multiplication routines, which would make your whole network significantly slower. Use the native array objects and create a multi layer abstraction on top of them.

But actually if you want speed and usability (and to really build some NN models), you should consider using something like R interface to TensorFlow. As a bonus you'll get things like running on the GPU for free.

Answer 4

Nice puzzle.. If you are asking calculating index in which would happen in runtime for which it needs to be compiled. Just want to understand how would you let the compiler compute it? IF you have a need to playing with the info anytime later then I would suggest to use Hasmap kind of mechanism. I had done it for a similar need.