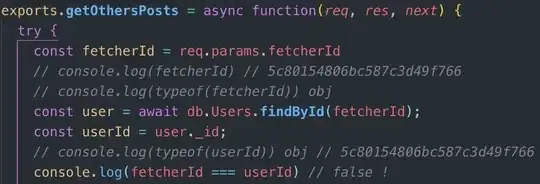
I'm learning C programming and made the algorithm below to solve this problem:
 The code actually works, but initially the loop was with only 10 repetitions (rep <= 10), and the anwer for p = 3 was almost correct, so I changed rep <= 20. And It gave me just the exact answer from my calculator. And then I tried with a higher number, 12, and the output again was inaccurate. So I ended raising rep <= 35. If I get the loop for higher repetitions I get "-nan", and if the input for p is too high it will be the same. So just have to see the pattern to know that the problem of inaccuracy will get back as I input higher numbers which is not the case because the output will be NaN if I input a high value.
The code actually works, but initially the loop was with only 10 repetitions (rep <= 10), and the anwer for p = 3 was almost correct, so I changed rep <= 20. And It gave me just the exact answer from my calculator. And then I tried with a higher number, 12, and the output again was inaccurate. So I ended raising rep <= 35. If I get the loop for higher repetitions I get "-nan", and if the input for p is too high it will be the same. So just have to see the pattern to know that the problem of inaccuracy will get back as I input higher numbers which is not the case because the output will be NaN if I input a high value.
Is it possible to solve it without higher level functions? just want to know if my program is ok for the level in which I am now...
#include <stdio.h>
int main()
{
float p; //the power for e
float power; //the copy of p for the loop
float e = 1; //the e number I wanna raise to the power of p
int x = 1; //the starting number for each factorial generation
float factorial = 1;
int rep = 1; //the repeater for the loop
printf( "Enter the power you want to raise: " );
scanf( "%f", &p );
power = p;
while ( rep <= 35) {
while ( x > 1) {
factorial *= x;
x--;
}
e += p / factorial;
//printf("\nthe value of p: %f", p); (TESTER)
//printf("\nthe value of factorial: %f", factorial); (TESTER)
p *= power; //the new value for p
rep++;
factorial = 1;
x = rep; //the new value for the next factorial to be generated
//printf("\n%f", e); (TESTER)
}
printf("%.3f", e);
return 0;
}
Sorry if I had syntax/orthography errors, I'm still learning the language.