How to vary the velocity around an ellipse

Question

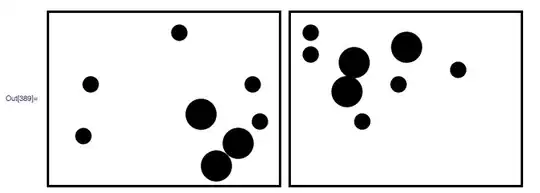
I have a c++ program that creates a list of offsets that correspond to traversing around an ellipse. I need to vary the velocity so that more time (i.e. more of the produced offsets) are near the far ends of the oval. The oval is long and skinny, and the current way I am calculating the offsets results in more offsets near the center of the ellipse, which is the opposite of what i want.

code:

// breathingPeriod, intervalMS, and yRadius are variables.
// Good defaults are: breathingPeriod = 5, intervalMs = 10, yRadius = 20
const int points = breathingPeriod * 1000 / intervalMS;
const double velocityCoeff = 360 / (breathingPeriod * 1000);
const zRadius = 3;
std::ofstream out("output.txt");


for(int i = 0; i < points; ++i)
{
    const int age = intervalMS * i;
    const uint64_t thetaDeg = static_cast<uint64_t>(age * velocityCoeff) % 360;
    const double thetaRad = thetaDeg * M_PI / 180.0;
    const double tanTheta = tan(thetaRad);
    double zOffset= (yRadius* zRadius) / sqrt(pow(yRadius, 2) + pow(zRadius, 2) * pow(tanTheta, 2));

    if(thetaRad > M_PI_2 && thetaRad <= 3 * M_PI_2)
    {
        zOffset = -zOffset;
    }
    const double yOffset = zOffset * tanTheta;
    double xOffset = 0;
    std::string str;
    str += std::to_string(xOffset) + " " + std::to_string(yOffset) + " " + std::to_string(zOffset) + "\n";

    out << str;
}
out.close;

I have tried varying the velocity based on cos of the previous angle, but i have yet to get that to work successfully.

While the movement is similar to an orbit, It doesn't need to follow most of the rules orbits do. Also, the input parameters are completely different from a normal orbital mechanics equation, and the objective is to create offsets for a single object over time, rather than to figure out the position of a large number of objects given an observer position and a database of stellar coordinates.

Answer 1

It sounds from your question as though you'd like a way of tuning the spacing of sample points around the ellipse, rather than having a particular physical system that is generating an orbit. Obviously, if you have an elliptical orbit defined by a gravitational field, then the equations for that are well known, and provide a fixed relationship between the velocity and position as functions of time.

If all you want is a tunable spacing of your points around the ellipse, then one way you can achieve this is simply to have your "angle" parameter varying non-linearly, but in a way that still guarantees to monotonically cover the range [0,2*pi]. Suppose that you have a "time" coordinate that covers the range [0,2*pi], but your "angle" is defined by the following relation:

where the skewness parameter, a, must be in the range (-0.5, 0.5) to ensure that the angle does not backtrack at any point on the curve. If a=0.3, this produces a trend like this:

where the gradient of the curve is steepest near where theta is a multiple of pi, and shallowest near odd multiples of pi/2.

Your ellipse can then be generated by the usual recipe:

Suppose we generate a sequence of 100 points uniformly spaced in t, and start with a=0, then we get a profile like this:

If we increase a to 0.2, we get points that become more tightly grouped near the y-axis:

Increasing a still further to 0.48, we get an even tighter bunching:

In Python, this can be implemented by something like the following:

import numpy

xRadius = 10
yRadius = 5
skew = 0.48

t = numpy.linspace(0, 2 * numpy.pi, 100)
theta = t + skew * numpy.sin(2*t)
x = xRadius * numpy.cos(theta)
y = yRadius * numpy.sin(theta)

Obviously, the corresponding code in C++ is more verbose, but straightforward to implement.