I am using OpenCV to estimate a webcam's intrinsic matrix from a series of chessboard images - as detailed in this tutorial, and reverse project a pixel to a direction (in term of azimuth/elevation angles).
The final goal is to let the user select a point on the image, estimate the direction of this point in relation to the center of the webcam, and use this as DOA for a beam-forming algorithm.
So once I have estimated the intrinsic matrix, I reverse project the user-selected pixel (see code below) and display it as azimuth/elevation angles.
result = [0, 0, 0] # reverse projected point, in homogeneous coord.
while 1:
_, img = cap.read()
if flag: # If the user has clicked somewhere
result = np.dot(np.linalg.inv(mtx), [mouse_x, mouse_y, 1])
result = np.arctan(result) # convert to angle
flag = False
cv2.putText(img, '({},{})'.format(mouse_x, mouse_y), (20, 440), cv2.FONT_HERSHEY_SIMPLEX,
0.5, (0, 255, 0), 2, cv2.LINE_AA)
cv2.putText(img, '({:.2f},{:.2f})'.format(180/np.pi*result[0], 180/np.pi*result[1]), (20, 460),
cv2.FONT_HERSHEY_SIMPLEX, 0.5, (0, 255, 0), 2, cv2.LINE_AA)
cv2.imshow('image', img)
if cv2.waitKey(1) & 0xFF == ord('q'):
break
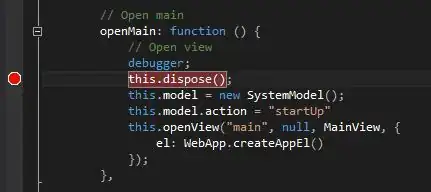
My problem is that I'm not sure whether my results are coherent. The major incoherence is that, the point of the image corresponding to the {0,0} angle is noticeably off the image center, as seen below (camera image has been replaced by a black background for privacy reasons) :
I don't really see a simple yet efficient way of measuring the accuracy (the only method I could think of was to use a servo motor with a laser on it, just under the camera and point it to the computed direction).
Here is the intrinsic matrix after calibration with 15 images :
I get an error of around 0.44 RMS which seems satisfying.
My calibration code :
nCalFrames = 12 # number of frames for calibration
nFrames = 0
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001) # termination criteria
objp = np.zeros((9*7, 3), np.float32)
objp[:, :2] = np.mgrid[0:9, 0:7].T.reshape(-1, 2)
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
cap = cv2.VideoCapture(0)
previousTime = 0
gray = 0
while 1:
# Capture frame-by-frame
_, img = cap.read()
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Find the chess board corners
ret, corners = cv2.findChessboardCorners(gray, (9, 7), None)
# If found, add object points, image points (after refining them)
if ret:
corners2 = cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)
if time.time() - previousTime > 2:
previousTime = time.time()
imgpoints.append(corners2)
objpoints.append(objp)
img = cv2.bitwise_not(img)
nFrames = nFrames + 1
# Draw and display the corners
img = cv2.drawChessboardCorners(img, (9, 7), corners, ret)
cv2.putText(img, '{}/{}'.format(nFrames, nCalFrames), (20, 460), cv2.FONT_HERSHEY_SIMPLEX,
2, (0, 255, 0), 2, cv2.LINE_AA)
cv2.putText(img, 'press \'q\' to exit...', (255, 15), cv2.FONT_HERSHEY_SIMPLEX,
0.5, (0, 0, 255), 1, cv2.LINE_AA)
# Display the resulting frame
cv2.imshow('Webcam Calibration', img)
if nFrames == nCalFrames:
break
if cv2.waitKey(1) & 0xFF == ord('q'):
break
RMS_error, mtx, disto_coef, _, _ = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1], None, None)
EDIT: another test method would be to use a whiteboard with known angles points and estimate the error by comparing with experimental results, but I don't know how to set up such a system