1

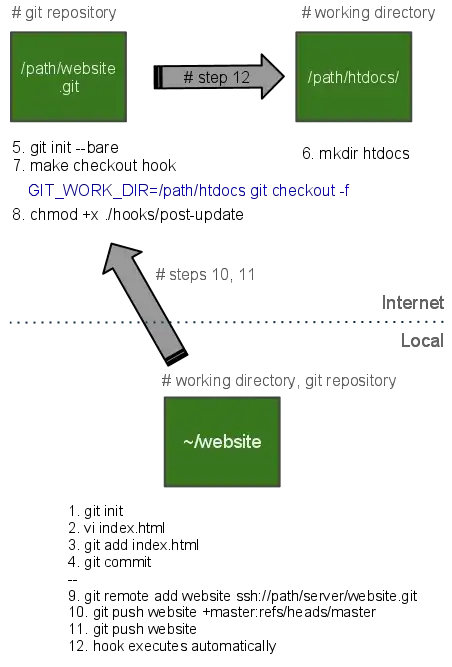
I'm learning algorithms now, and while implementing red-black tree insertion I came up to the idea described in the question's header. This takes place when equal value nodes are involved.

Let's start with a simple example tree, where left children are less than the parent and right children are greater or equal to the parent.

Initial state of such tree might be the following:

start

Then, if I rotate this tree left, I get:

enter image description here

The node which violates the BST condition that all left children are less than the parent is shown in red.

So the question is: why lots of algorithms which implement insertion, deletion or else on binary search trees use rotation when rotations break BSTs (or do I just do the rotation wrong)?

Denis Seletkov
  • 49
  • 5
  • 5
    Trees which do not allow duplicates typically have the condition you describe. Trees that allow duplicates normally relax this to "all left children are less-than-or-equal". – Hitobat Apr 01 '18 at 19:38
  • If this strict inequality condition exists, what's to say that the equivalent condition for *right* children does not? – meowgoesthedog Apr 01 '18 at 20:12
  • The tree is only broken because you say it's broken. Algorithms that use rotations would not have such conditions. – Matt Timmermans Apr 02 '18 at 05:33

2 Answers2

2

The question is why you want to rotate your BST when it satisfies all conditions. The rotation in your example will not be implemented in any sense. In 'lots of algorithms', the rotation is only required when 'insertion' or 'deletion' or 'else' makes a new tree that violates BST properties. Lets say if you replace 6 by 8 as the root of BST, now your rotation will make sense.

tudatn
  • 102
  • 1
  • 6
  • You shouldn't be distracted by this particular case, the problem is still there. Imagine adding 8 to the tree described in the question, and you'll have to do the same rotation to balance the tree. – Denis Seletkov Apr 03 '18 at 16:44
  • Perfect, so you have a balance tree as you want with rotations. I mentioned your example to just illustrate a point that you deliberately do rotation on your BST when there is no violation of your defined BST. It will not happen in any algorithms. – tudatn Apr 03 '18 at 17:24
0

To the best of my knowledge, most textbooks introduce BSTs by considering unique keys, that is: left < root < right. Everything is based on this, including rotations. How to deal with duplicates is usually left as an exercise, and no one says it has to be as simple as just changing that invariant to left <= root < right.

This is done exactly because of the problem you describe: in some cases, rotations might not work "out of the box" with duplicates. There's probably always a way to make them work even if you add duplicate nodes (and don't resort to storing a count in each node), but it would just distract from the general idea to have to mention that edge case and its solution for various trees involving rotations.

So basically:

  • Depending on your tree, rotations might not always work the "standard" way described in a textbook if you change the textbook's preconditions: if the textbook says left < root < right, you shouldn't assume its algorithms also work as given for left <= root < right or any other precondition. You might need to change some things. In RB trees for example, you might need to do the rotation at a lower level.
  • If you don't want to bother changing anything, just add another field in your node that counts how many times that node's key appears.
IVlad
  • 43,099
  • 13
  • 111
  • 179