Solving a first order system of ODEs using SymPy expressions and SciPy solver

Question

I am trying to learn how to integrate python SymPy with SciPy for numerically solving ordinary differential equations. However, I was kinda lost about how to actually get the SymPy form of a first order system of ODEs into a format that I can process with scipy.integrate.odeint()

Note, some people suggested that this is similar to another post, but that is not the case. The other post is here.
Convert sympy expressions to function of numpy arrays

So this other post is a much more complicated case where the user wants to accelerate computation of an ODE using Theano or some other libraries. I am just trying to understand the basic interface between SymPy and SciPy, so this other post is not at all helpful.

As a toy example, I was using the Lotka-Volterra equation to test the use of SymPy. The equations are:

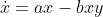
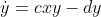
I can solve this in the conventional way with Scipy and it works. Here is the working code.

import numpy as np
import scipy
from scipy.integrate import odeint, ode, solve_ivp
import sympy
import matplotlib.pyplot as plt
sympy.init_printing()

def F_direct(X, t, args):
    F = np.zeros(2)
    a, b, c, d = args
    x,y = X
    F[0] = a*x - b*x*y
    F[1] = c*x*y- d*y
    return F

argst = [0.4,0.002,0.001,0.7]
xy0 = [600, 400]
t = np.linspace(0, 50, 250)
xy_t, infodict = odeint(F_direct, xy0, t, args=(argst,), full_output=True)

plt.plot(t, xy_t[:,1], 'o', t, xy_t[:,0])
plt.grid(True)
plt.xlabel('x'); plt.ylabel('y')
plt.legend(('Numerical', 'Exact'), loc=0)
plt.show()

Now I was kind lost about how to do this with SymPy. I have a sense of what needs to be done, but was not sure how to proceed. The only example I have found is way too complicated to learn from. Here is what I have.

x, y, a, b, c, d = sympy.symbols('x y a b c d')
t = np.linspace(0, 50, 250)
ode1 = sympy.Eq(a*x - b*x*y)
ode2 = sympy.Eq(c*x*y - d*y)

I am supposed to put these equations into some sort of system form and then use the sympy.lambdify function to return a new function that I can pass to odeint

So can anyone fill in the blanks here on how I set up this ode1,ode2 system to process with SymPy.

Answer 1

There is rarely need to use Eq objects in SymPy; equations are best represented by expressions, which are understood to be equated to zero in the context of solvers. So, ode1 and ode2 should just be expressions for the right-hand side of the ODE system. Then they can be lambdified together, as follows:

ode1 = a*x - b*x*y
ode2 = c*x*y - d*y
F_sympy = sympy.lambdify((x, y, a, b, c, d), [ode1, ode2])
def F_from_sympy(X, t, args):
    a, b, c, d = args
    x, y = X    
    return F_sympy(x, y, a, b, c, d)

The additional step after lambdification is needed because SciPy's solver passes some arrays, which the lambdified function will not know how to unpack. Example:

F_from_sympy([1, 2], np.linspace(0, 1, 100), (3, 4, 5, 6))

returns [-5, -2] which is a Python list rather than a NumPy array, but the ODE solver should handle that. (Or you can return np.array(F_sympy(x, y, a, b, c, d))).)

Answer 2

I wrote a module named JiTCODE, which creates ODE integrator objects (with a handling similar to scipy.integrate.ode) from symbolic expressions (SymPy or SymEngine) describing the right-hand side. Under the hood it uses scipy.integrate.ode and scipy.integrate.solve_ivp for the integration.

The only drawback in your case is that the symbol for the dynamical variables and time is prescribed, so you might have to do a symbolic substitution – which should not be a big issue, however. Below, is your Lotka–Volterra equation as an example, using y(0) instead of x and y(1) instead of y.

import numpy as np
from sympy.abc import a,b,c,d
from jitcode import y, jitcode

xy0 = [600,400]
argst = [0.4,0.002,0.001,0.7]

lotka_volterra = [
         a*y(0) - b*y(0)*y(1),
        -d*y(1) + c*y(0)*y(1)
    ]

ODE = jitcode( lotka_volterra, control_pars=[a,b,c,d] )
ODE.set_integrator("dopri5")
ODE.set_initial_value(xy0)
ODE.set_parameters(*argst)

times = np.linspace(0, 50, 250)
xy_t = np.vstack(ODE.integrate(time) for time in times)

Note that the main feature of this module is that the right-hand side is compiled for efficiency. Depending on what you need to do, this may be overkill, but it doesn’t harm if it works (you can also disable this and use lambdification as detailed in the other answer).