Displaying orthographic views of a rotating cube in C++

Question

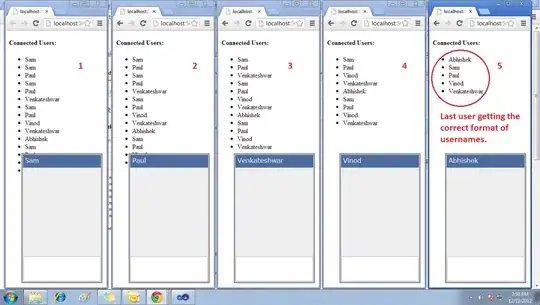
The code below is to display the orthographic projections(side view, front view and top view) of a rotating cube. The approach I have taken is homogenous coordinates. I take on displaying each edge of the cube, as for side view, I haven't considered the x components of cube vertices and drawn edges using only y and z components. This shows the other side faces too, how can I detect only the left side faces?

#include<iostream>
#include "graphics.h"
#include<cmath>
using namespace std;

#define PI 22/(float)7

float x =0, y = 0, z= 0;

void matrixmult(int A[4][8], float R[4][4]){
    float res[4][8];
    for(int i = 0; i<4; i++){
        for(int j = 0; j<8; j++){
            res[i][j] = 0;
            for(int k = 0; k<4; k++){
                res[i][j]+=R[i][k]*A[k][j];
            }
        }
    }
    for(int i = 0; i<4; i++){
        for(int j = 0; j<8; j++){
            A[i][j] = res[i][j];
        }
    }
}

void rotMataboutX(float Rx[4][4]){
   float  xrad = PI*x/(float)360;
   float cosx = cos(xrad), sinx = sin(xrad);
    Rx[1][1]=cosx;
    Rx[1][2]=-sinx;
    Rx[2][1]=sinx;
    Rx[2][2]=cosx;
}

void rotMatAboutY(float Ry[4][4]){
    float  yrad = PI*y/(float)360;
    float cosy = cos(yrad), siny = sin(yrad);
    Ry[0][0]=cosy;
    Ry[0][2]=siny;
    Ry[2][0]=-siny;
    Ry[2][2]=cosy;
}

void rotMatAboutZ(float Rz[4][4]){
    float  zrad = PI*z/(float)360;
    float cosz = cos(zrad), sinz = sin(zrad);
    Rz[0][0]=cosz;
    Rz[0][1]=-sinz;
    Rz[1][0]=sinz;
    Rz[1][1]=cosz;
}

void sideView(int A[4][8]){
    int xdisp = 106, ydisp = 120;
    line(xdisp+A[1][0], ydisp+A[2][0], xdisp+A[1][1], ydisp+A[2][1]);
    line(xdisp+A[1][1], ydisp+A[2][1], xdisp+A[1][2], ydisp+A[2][2]);
    line(xdisp+A[1][2], ydisp+A[2][2], xdisp+A[1][3], ydisp+A[2][3]);
    line(xdisp+A[1][3], ydisp+A[2][3], xdisp+A[1][0], ydisp+A[2][0]);
    line(xdisp+A[1][4], ydisp+A[2][4], xdisp+A[1][5], ydisp+A[2][5]);
    line(xdisp+A[1][5], ydisp+A[2][5], xdisp+A[1][6], ydisp+A[2][6]);
    line(xdisp+A[1][6], ydisp+A[2][6], xdisp+A[1][7], ydisp+A[2][7]);
    line(xdisp+A[1][7], ydisp+A[2][7], xdisp+A[1][4], ydisp+A[2][4]);
    line(xdisp+A[1][0], ydisp+A[2][0], xdisp+A[1][4], ydisp+A[2][4]);
    line(xdisp+A[1][1], ydisp+A[2][1], xdisp+A[1][5], ydisp+A[2][5]);
    line(xdisp+A[1][6], ydisp+A[2][6], xdisp+A[1][2], ydisp+A[2][2]);
    line(xdisp+A[1][7], ydisp+A[2][7], xdisp+A[1][3], ydisp+A[2][3]);
    line(xdisp+A[1][7], ydisp+A[2][7], xdisp+A[1][3], ydisp+A[2][3]);
}

void frontView(int A[4][8]){
    int xdisp = 319, ydisp = 120;
    line(xdisp+A[0][0], ydisp+A[1][0], xdisp+A[0][1], ydisp+A[1][1]);
    line(xdisp+A[0][1], ydisp+A[1][1], xdisp+A[0][2], ydisp+A[1][2]);
    line(xdisp+A[0][2], ydisp+A[1][2], xdisp+A[0][3], ydisp+A[1][3]);
    line(xdisp+A[0][3], ydisp+A[1][3], xdisp+A[0][0], ydisp+A[1][0]);
    line(xdisp+A[0][4], ydisp+A[1][4], xdisp+A[0][5], ydisp+A[1][5]);
    line(xdisp+A[0][5], ydisp+A[1][5], xdisp+A[0][6], ydisp+A[1][6]);
    line(xdisp+A[0][6], ydisp+A[1][6], xdisp+A[0][7], ydisp+A[1][7]);
    line(xdisp+A[0][7], ydisp+A[1][7], xdisp+A[0][4], ydisp+A[1][4]);
    line(xdisp+A[0][0], ydisp+A[1][0], xdisp+A[0][4], ydisp+A[1][4]);
    line(xdisp+A[0][1], ydisp+A[1][1], xdisp+A[0][5], ydisp+A[1][5]);
    line(xdisp+A[0][6], ydisp+A[1][6], xdisp+A[0][2], ydisp+A[1][2]);
    line(xdisp+A[0][7], ydisp+A[1][7], xdisp+A[0][3], ydisp+A[1][3]);
    line(xdisp+A[0][7], ydisp+A[1][7], xdisp+A[0][3], ydisp+A[1][3]);
}

void topView(int A[4][8]){
    int xdisp = 534, ydisp = 120;
    line(xdisp+A[0][0], ydisp+A[2][0], xdisp+A[0][1], ydisp+A[2][1]);
    line(xdisp+A[0][1], ydisp+A[2][1], xdisp+A[0][2], ydisp+A[2][2]);
    line(xdisp+A[0][2], ydisp+A[2][2], xdisp+A[0][3], ydisp+A[2][3]);
    line(xdisp+A[0][3], ydisp+A[2][3], xdisp+A[0][0], ydisp+A[2][0]);
    line(xdisp+A[0][4], ydisp+A[2][4], xdisp+A[0][5], ydisp+A[2][5]);
    line(xdisp+A[0][5], ydisp+A[2][5], xdisp+A[0][6], ydisp+A[2][6]);
    line(xdisp+A[0][6], ydisp+A[2][6], xdisp+A[0][7], ydisp+A[2][7]);
    line(xdisp+A[0][7], ydisp+A[2][7], xdisp+A[0][4], ydisp+A[2][4]);
    line(xdisp+A[0][0], ydisp+A[2][0], xdisp+A[0][4], ydisp+A[2][4]);
    line(xdisp+A[0][1], ydisp+A[2][1], xdisp+A[0][5], ydisp+A[2][5]);
    line(xdisp+A[0][6], ydisp+A[2][6], xdisp+A[0][2], ydisp+A[2][2]);
    line(xdisp+A[0][7], ydisp+A[2][7], xdisp+A[0][3], ydisp+A[2][3]);
    line(xdisp+A[0][7], ydisp+A[2][7], xdisp+A[0][3], ydisp+A[2][3]);
}

int main(){
    int gd = DETECT, gm;
    initgraph(&gd, &gm, "C:\\TC\\BGI");
    int A[4][8]={{0, 50, 50, 0, 0, 50, 50, 0},
                {0, 0, 50, 50, 0, 0, 50, 50},
                {0, 0, 0, 0, 50, 50, 50, 50},
                {1, 1, 1 ,1 ,1 ,1, 1, 1}};


    float cosx = cos(x), sinx = sin(x);
    float Rx[4][4]={{1, 0, 0, 0},
            {0, cosx, -sinx, 0},
            {0, sinx, cosx, 0},
            {0, 0, 0, 1}};

    float cosy = cos(y), siny = sin(y);
    float Ry[4][4]={{cosy, 0, siny, 0},
            {0, 1, 0, 0},
            {-siny, 0, cosy, 0},
            {0, 0, 0, 1}};

    float cosz = cos(z), sinz = sin(z);
    float Rz[4][4]={{cosz, -sinz, 0, 0},
            {sinz, cosz, 0, 0},
            {0, 0, 1, 0},
            {0, 0, 0, 1}};

    cout<<"Matrix A:\n";
     for(int i = 0; i<4; i++){
        for(int j = 0; j<8; j++){
            cout<<A[i][j]<<" ";
        }
        cout<<endl;
    }
    sideView(A);
    topView(A);
    frontView(A);

    while(1){
        char axisofrot;
        cin>>axisofrot;
        switch(axisofrot){
        case 'X':
        case 'x':
            cout<<"ROTATING ABOUT X:\n";
            x+=5;
            cout<<"X:\t"<<x<<"\n";
            cout<<"Y:\t"<<y<<"\n";
            cout<<"Z:\t"<<z<<"\n";
            rotMataboutX(Rx);
            cout<<"Matrix Rx:\n";
            for(int i = 0; i<4; i++){
                for(int j = 0; j<4; j++){
                    cout<<Rx[i][j]<<" ";
                }
                cout<<endl;
            }
            matrixmult(A, Rx);
            break;
        case 'Y':
        case 'y':
            cout<<"ROTATING ABOUT Y:\n";
            y+=5;
            cout<<"X:\t"<<x<<"\n";
            cout<<"Y:\t"<<y<<"\n";
            cout<<"Z:\t"<<z<<"\n";
            rotMatAboutY(Ry);
            cout<<"Matrix Ry:\n";
            for(int i = 0; i<4; i++){
                for(int j = 0; j<4; j++){
                    cout<<Ry[i][j]<<" ";
                }
                cout<<endl;
            }
            matrixmult(A, Ry);
            break;
        case 'Z':
        case 'z':
            cout<<"ROTATING ABOUT Z:\n";
            z+=5;
            cout<<"X:\t"<<x<<"\n";
            cout<<"Y:\t"<<y<<"\n";
            cout<<"Z:\t"<<z<<"\n";
            rotMatAboutY(Rz);
            cout<<"Matrix Rz:\n";
            for(int i = 0; i<4; i++){
                for(int j = 0; j<4; j++){
                    cout<<Rz[i][j]<<" ";
                }
                cout<<endl;
            }
            matrixmult(A, Rz);
            break;
        }
        cout<<"Matrix A:\n";
        for(int i = 0; i<4; i++){
            for(int j = 0; j<8; j++){
                cout<<A[i][j]<<" ";
            }
            cout<<endl;
        }
        cleardevice();
        delay(100);
        sideView(A);
        topView(A);
        frontView(A);
    }
    getch();
    closegraph();
    return 0;
}

Initially, without rotation

After rotating by 20 degrees along x, y and z axes

Your orthographic views don't look right. Read up about projection matrices and backface culling. — meowgoesthedog, Apr 15 '18 at 01:02

score 0 · Answer 1 · answered Apr 15 '18 at 06:47

What you need is to use normals and back face culling. So if you define normal vector n pointing out of your cube for each face than:

if (dot ( n , camera_view_direction) < 0) render_face;

will decide if you are rendering front or back face. Both vectors must be in the same coordinate system so either transform n or the camera view or both ... Do not forget that transforming vectors is done without offset !!!

If you do not have normals n you can compute them on the run for each face defined by points p0,p1,p2,... like this:

n = cross (p1-p0,p2-p1)

but the orientation if it points in or out will depends on winding rule of your face, cross operand order and your coordinate system conventions. So tweak to match your needs (it is good idea to render the normals to visually see if they correct)

also take a look at this:

Understanding 4x4 homogenous transform matrices

For additional ideas stuff and math. All the views and transforms can be represented by 4x4 matrix and you can get rid of your projection functions and use just matrices instead.

Displaying orthographic views of a rotating cube in C++

1 Answers1