Generating random floating-point values based on random bit stream

Question

Given a random source (a generator of random bit stream), how do I generate a uniformly distributed random floating-point value in a given range?

Assume that my random source looks something like:

unsigned int GetRandomBits(char* pBuf, int nLen);

And I want to implement

double GetRandomVal(double fMin, double fMax);

Notes:

• I don't want the result precision to be limited (for example only 5 digits).
• Strict uniform distribution is a must
• I'm not asking for a reference to an existing library. I want to know how to implement it from scratch.
• For pseudo-code / code, C++ would be most appreciated

Answer 1

I don't think I'll ever be convinced that you actually need this, but it was fun to write.

#include <stdint.h>

#include <cmath>
#include <cstdio>

FILE* devurandom;

bool geometric(int x) {
  // returns true with probability min(2^-x, 1)
  if (x <= 0) return true;
  while (1) {
    uint8_t r;
    fread(&r, sizeof r, 1, devurandom);
    if (x < 8) {
      return (r & ((1 << x) - 1)) == 0;
    } else if (r != 0) {
      return false;
    }
    x -= 8;
  }
}

double uniform(double a, double b) {
  // requires IEEE doubles and 0.0 < a < b < inf and a normal
  // implicitly computes a uniform random real y in [a, b)
  // and returns the greatest double x such that x <= y
  union {
    double f;
    uint64_t u;
  } convert;
  convert.f = a;
  uint64_t a_bits = convert.u;
  convert.f = b;
  uint64_t b_bits = convert.u;
  uint64_t mask = b_bits - a_bits;
  mask |= mask >> 1;
  mask |= mask >> 2;
  mask |= mask >> 4;
  mask |= mask >> 8;
  mask |= mask >> 16;
  mask |= mask >> 32;
  int b_exp;
  frexp(b, &b_exp);
  while (1) {
    // sample uniform x_bits in [a_bits, b_bits)
    uint64_t x_bits;
    fread(&x_bits, sizeof x_bits, 1, devurandom);
    x_bits &= mask;
    x_bits += a_bits;
    if (x_bits >= b_bits) continue;
    double x;
    convert.u = x_bits;
    x = convert.f;
    // accept x with probability proportional to 2^x_exp
    int x_exp;
    frexp(x, &x_exp);
    if (geometric(b_exp - x_exp)) return x;
  }
}

int main() {
  devurandom = fopen("/dev/urandom", "r");
  for (int i = 0; i < 100000; ++i) {
    printf("%.17g\n", uniform(1.0 - 1e-15, 1.0 + 1e-15));
  }
}

Answer 2

Here is one way of doing it.

The IEEE Std 754 double format is as follows:

[s][     e     ][                          f                         ]

where s is the sign bit (1 bit), e is the biased exponent (11 bits) and f is the fraction (52 bits).

Beware that the layout in memory will be different on little-endian machines.

For 0 < e < 2047, the number represented is

(-1)**(s)   *  2**(e – 1023)  *  (1.f)

By setting s to 0, e to 1023 and f to 52 random bits from your bit stream, you get a random double in the interval [1.0, 2.0). This interval is unique in that it contains 2 ** 52 doubles, and these doubles are equidistant. If you then subtract 1.0 from the constructed double, you get a random double in the interval [0.0, 1.0). Moreover, the property about being equidistant is preserve. From there you should be able to scale and translate as needed.

Answer 3

I'm surprised that for question this old, nobody had actual code for the best answer. User515430's answer got it right--you can take advantage of IEEE-754 double format to directly put 52 bits into a double with no math at all. But he didn't give code. So here it is, from my public domain ojrandlib:

double ojr_next_double(ojr_generator *g) {
    uint64_t r = (OJR_NEXT64(g) & 0xFFFFFFFFFFFFFull) | 0x3FF0000000000000ull;
    return *(double *)(&r) - 1.0;
}

NEXT64() gets a 64-bit random number. If you have a more efficient way of getting only 52 bits, use that instead.

Answer 4

This is easy, as long as you have an integer type with as many bits of precision as a double. For instance, an IEEE double-precision number has 53 bits of precision, so a 64-bit integer type is enough:

#include <limits.h>
double GetRandomVal(double fMin, double fMax) {
  unsigned long long n ;
  GetRandomBits ((char*)&n, sizeof(n)) ;
  return fMin + (n * (fMax - fMin))/ULLONG_MAX ;
}

Answer 5

This is probably not the answer you want, but the specification here:

http://www.open-std.org/jtc1/sc22/wg21/docs/papers/2010/n3225.pdf

in sections [rand.util.canonical] and [rand.dist.uni.real], contains sufficient information to implement what you want, though with slightly different syntax. It isn't easy, but it is possible. I speak from personal experience. A year ago I knew nothing about random numbers, and I was able to do it. Though it took me a while... :-)

Answer 6

The question is ill-posed. What does uniform distribution over floats even mean?

Taking our cue from discrepancy, one way to operationalize your question is to define that you want the distribution that minimizes the following value:

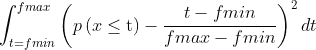
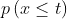Where x is the random variable you are sampling with your GetRandomVal(double fMin, double fMax) function, and means the probability that a random x is smaller or equal to t.

And now you can go on and try to evaluate eg a dabbler's answer. (Hint all the answers that fail to use the whole precision and stick to eg 52 bits will fail this minimization criterion.)

However, if you just want to be able to generate all float bit patterns that fall into your specified range with equal possibility, even if that means that eg asking for GetRandomVal(0,1000) will create more values between 0 and 1.5 than between 1.5 and 1000, that's easy: any interval of IEEE floating point numbers when interpreted as bit patterns map easily to a very small number of intervals of unsigned int64. See eg this question. Generating equally distributed random values of unsigned int64 in any given interval is easy.

Answer 7

I may be misunderstanding the question, but what stops you simply sampling the next n bits from the random bit stream and converting that to a base 10 number number ranged 0 to 2^n - 1.

Answer 8

To get a random value in [0..1[ you could do something like:

double value = 0;
for (int i=0;i<53;i++)
   value = 0.5 * (value + random_bit());  // Insert 1 random bit
   // or value = ldexp(value+random_bit(),-1);
   // or group several bits into one single ldexp
return value;