A PCFG defines (i) a distribution over parse trees and (ii) a distribution over sentences.
The probability of a parse tree given by a PCFG is:
where the parse tree t is described as a multiset of rules r (it is a multiset because a rule can be used several times to derive a tree).
To compute the probability of a sentence, you have to consider every possible way of deriving the sentence and sum over their probabilities.
where 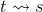 means that the string of terminals (the yield) of t is the sentence s.
means that the string of terminals (the yield) of t is the sentence s.
In your example, the probability of "what is a cat" is 0 because you cannot generate it with your grammar. Here's another example with a toy grammar:
Rule Probability
S -> NP VP 1
NP -> they 0.5
NP -> fish 0.5
VP -> VBP NP 0.5
VP -> MD VB 0.5
VBP -> can 1
MD -> can 1
VB -> fish 1
The sentence "they can fish" has two possible parse trees:
(S (NP they) (VP (MD can) (VB fish)))
(S (NP they) (VP (VBP can) (NP fish)))
with probabilities:
S NP VP MD VB
1 * 0.5 * 0.5 * 1 * 1 = 1 / 4
and
S NP VP VBP NP
1 * 0.5 * 0.5 * 1 * 0.5 = 1 /8
so its probability is the sum or probabilities of both parse trees (3/8).
It turns out that in the general case, it is too computationally expensive to enumerate each possible parse tree for a sentence.
However, there is a O(n^3) algorithm to compute the sum efficiently: the inside-outside algorithm (see pages 17-18), pdf by Michael Collins.
Edit: corrected trees.


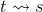 means that the string of terminals (the yield) of t is the sentence s.
means that the string of terminals (the yield) of t is the sentence s.