Make object orbit around another with Degrees only (Not radians only integer math)

Question

I'm currently developing something that requires objects to orbit around another. Though, I am limited. I cannot use Radians to achieve this. I have access to sin and cos, and the degrees. But I cannot use radians (it breaks everything). Note that this is within Minecraft and the values there cannot hold floats or doubles. So, an answer like 0.017 will be 17. For this reason, I cannot use radians.

The function to calculate sin and cos is limited between -180 to 180. This means I cannot simply turn 0.787 radians into 787 radians, as that's out of the limit, and the answer returned would be completely wrong.

Right now the code would be something like this:

var distance = 100; // from the centre of orbit
var degrees = 45; // around a 360 degree orbit
var radians = degrees * (Math.PI / 180);

var x = Math.cos(radians) * distance;
var y = Math.sin(radians) * distance;

But that code completely relies on degrees being converted into radians. I cannot do this, because of Minecraft's integer limits, and how the functions calculate sin and cos. It just is simply not possible.

So the main questions is: How can I find future position of an object with just the degrees, sin and cos? (Perhaps base the answer as if the degrees were 45 for instance)

Here is a great example picture:

Answer 1

why not make your own LUT in fixed point ? something like this in C++:

const int fp=1000; // fixed point precision
const int mycos[360]={ 1000, 999, 999, 998, 997, 996, 994, 992, 990, ... }

float x,y,x0=0,y0=0,r=50,ang=45;
x = x0 + ( (r*mycos[ ang    %360]) / fp );
y = y0 + ( (r*mycos[(ang+90)%360]) / fp );

Also you can write a script that will create the LUT for you. Each value in the LUT is computed like this:

LUT[i] = fp*cos(i*M_PI/180); // i = 0,1,2,...359

Now to normalize angle before use:

ang %= 360;
if (ang<0) ang+=360;

There are also ways to compute sin,cos tables with integer variables only out there. We used it in 8-bit era asm on Z80 for our stuff and later on x86 demos ... so it is possible to write code that would create it directly in minecraft script without the need of another compiler use.

You can even change the angular units to power of 2 instead of 360 so you can get rid of the modulo and also set the fp to mower of 2 -1 so you do not need even to divide. After some digging in my source archives I found my ancient TASM MS-DOS demo which uses this technique. After porting it to C++ and tweaking the constants here C++ result:

int mysinLUT[256];
void mysin_init100() // <-100,+100>
    {
    int bx,si=620,cx=0,dx;  // si ~amplitude
    for (bx=0;bx<256;bx++)
        {
        mysinLUT[bx]=(cx>>8);
        cx+=si;
        dx=41*cx;
        if (dx<0) dx=-((-dx)>>16); else dx>>=16;
        si-=dx;
        }
    }
void mysin_init127() // <-127,+127>
    {
    int bx,si=793,cx=0,dx;  // si ~amplitude
    for (bx=0;bx<256;bx++)
        {
        mysinLUT[bx]=(cx>>8)+1;
        cx+=si;
        dx=41*cx;
        if (dx<0) dx=-((-dx)>>16); else dx>>=16;
        si-=dx;
        }
    }
int mysin(int a){ return mysinLUT[(a   )&255]; }
int mycos(int a){ return mysinLUT[(a+64)&255]; }

The constants are set so the sin[256] holds rough approximation of sinus within range <-100,+100> or <-127,+127> (depends on which init you call) and the angle period is 256 instead of 360. You need first call the mysin_init???(); once to init the LUT after that you can use mysin,mycos just do not forget to divide the final result by /100 or >>7.

When I render overlay of real and approximated circle using VCL:

void draw()
    {
    // select range
//  #define range100
    #define range127

    // init sin LUT just once
    static bool _init=true;
    if (_init)
        {
        _init=false;
        #ifdef range100
        mysin_init100();
        #endif
        #ifdef range127
        mysin_init127();
        #endif
        }

    int a,x,y,x0,y0,r;
    // clear screen
    bmp->Canvas->Brush->Color=clWhite;
    bmp->Canvas->FillRect(TRect(0,0,xs,ys));
    // compute circle size from window resolution xs,ys
    x0=xs>>1;
    y0=ys>>1;
    r=x0; if (r>y0) r=y0; r=(r*7)/10;
    // render real circle
    bmp->Canvas->Pen->Color=clRed;
    bmp->Canvas->Ellipse(x0-r,y0-r,x0+r,y0+r);
    // render approximated circle
    bmp->Canvas->Pen->Color=clBlack;
    for (a=0;a<=256;a++)
        {
        #ifdef range100
        x=x0+((r*mycos(a))/100);
        y=y0-((r*mysin(a))/100);
        #endif
        #ifdef range127
        // if >> is signed (copying MSB)
        x=x0+((r*mycos(a))>>7);
        y=y0-((r*mysin(a))>>7);
        // if >> is unsigned (inserting 0) and all circle points are non negative
//      x=( (x0<<7)+(r*mycos(a)) )>>7;
//      y=( (y0<<7)-(r*mysin(a)) )>>7;
        // this should work no matter what
//      x=r*mycos(a); if (x<0) x=-((-x)>>7); else x>>=7; x=x0+x;
//      y=r*mysin(a); if (y<0) y=-((-y)>>7); else y>>=7; y=y0-y;
        // this work no matter what but use signed division
//      x=x0+((r*mycos(a))/127);
//      y=y0-((r*mysin(a))/127);
        #endif
        if (!a) bmp->Canvas->MoveTo(x,y);
        else    bmp->Canvas->LineTo(x,y);
        }
    Form1->Canvas->Draw(0,0,bmp);
    //bmp->SaveToFile("out.bmp");
    }

the result looks like this:

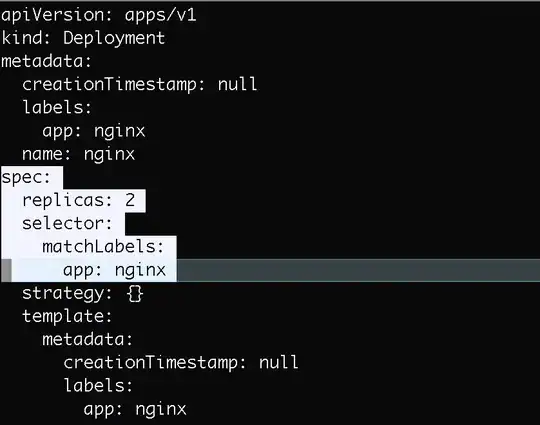
Red is real circle and Black is circle using mysin,mycos. As you can see there are small deviations due to approximations accuracy but no floating point operation is used here. It is weird as the 3 methods of bitshift rsults in different numbers (it must be some optimization of mine compiler) the constants are tweaked for the first method.