First method: with a table of constants.
First normalize the argument to a number between 1 and 2 (this is achieved by multiplying or dividing by 2 as many times as necessary - keep a count of these operations). For efficiency, if the values can span many orders of magnitude, instead of equal factors you can use a squared sequence, 2, 4, 16, 256..., followed by a dichotomic search when you have bracketed the value.
F.i. if the exponents 16=2^4 works but not 256=2^8, you try 2^6, then one of 2^5 and 2^7 depending on outcome. If the final exponent is 2^d, the linear search takes O(d) operations and the geometric/dichotomic search only O(log d). To avoid divisions, it is advisable to keep a table of negative powers.
After normalization, you need to refine the mantissa. Compare the value to √2, and if larger multiply by 1/√2. This brings the value between 1 and √2. Then compare to √√2 and so on. As you go, you add the weights 1/2, 1/4, ... to the exponent when a comparison returns greater.
In the end, the exponent is the base 2 logarithm.
Example: lg 27
27 = 2^4 x 1.6875
1.6875 > √2 = 1.4142 ==> 27 = 2^4.5 x 1.1933
1.1933 > √√2 = 1.1892 ==> 27 = 2^4.75 x 1.0034
1.0034 < √√√2 = 1.0905 ==> 27 = 2^4.75 x 1.0034
...
The true value is 4.7549.
Note that you can work with other bases, in particular e. In some contexts, base 2 allows shortcuts, this is why I used it. Of course, the square roots should be tabulated.
Second method: with a Taylor series.
After the normalization step, you can use the standard series
log(1 + x) = x - x²/2 + x³/3 - ...
which converges for |x| < 1. (Caution: we now have natural logarithms.)
As convergence is too slow for values close to 1, it is advisable to use the above method to reduce to the range [1, √2). Then every new term brings a new bit of accuracy.
Alternatively, you can use the series for log((1 + x)/(1 - x)), which gives a good convergence speed even for the argument 2. See https://fr.wikipedia.org/wiki/Logarithme_naturel#D%C3%A9veloppement_en_s%C3%A9rie
Example: with x = 1.6875, y = 0.2558 and
2 x (0.2558 + 0.2558³/3 + 0.2558^5/5) = 0.5232
lg 27 ~ 4 + 0.5232 / ln 2 = 4.7548
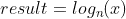
 stands for the logarithmBase and
stands for the logarithmBase and 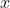 stands for the value.
stands for the value.