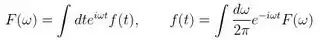The Fourier transform operations defined in Wikipedia are
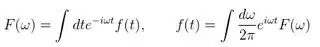
which is analogous to the numerical algorithms in Python (and Matlab).
However I want to use this alternative definition:
in order to numerically show that the following equations are FT pairs:
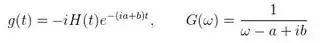
My Python code is adapted from my previous question Scaling problems with IFFT in Matlab. It performs FFT on g(t) and reverses the vector elements (code at bottom of post). Here is a plot of the analytical G(w) above compared to the fft solution and fft solution with the vector reversed.
It looks like there is agreement between the (reversed) numerical solution and G(w), but there is actually a large difference between them. It's like there needs to be an additional shift along the horizontal axis in order to get a more accurate result:
There are similar issues when I use IFFT to go from G(w) to g(t). So the question is, how do I implement this "alternative" definition of the FT? I'm not sure if my "vector reversal" method is appropriate. I suspect it has something to do with the phase of the FT.
Edit:
In response to Cris Luengo, I have fixed the typos in the FT relations above. In addition, it seems possible to implement the "alternative" FT by applying a simple substitution to Wikipedia's FT definition:

Long story short, I should use g(-t) in the FFT in order to get G(w). Does this sound logical? I tried this in my code and there is still a large discrepancy between the numerical and analytical result.
import numpy as np
from numpy.fft import fft,fftshift,ifft,ifftshift
import matplotlib.pyplot as plt
a = 3.119
b = 0.173
ts = 1e3 # time sampling
L = 500*ts # no. sample points
Ts = ts/L # sampling rate
Fs = 1/Ts # sampling frequency
f = (np.arange(-np.floor(L/2),(np.floor((L-1)/2)+1)))/L # digital (linear) freq
w = 2*np.pi*f # angular freq
t = np.arange(-L/2,L/2)*ts/L # time
H = lambda x:1*(x>0) # heaviside function
g = -1j*H(t)*np.exp(-(1j*a+b)*t) # test function for fft
Gn = 1/Fs*fftshift(fft(ifftshift(g))) # numerical fft
Gr = Gn[::-1] # reversed numerical result
Ga = 1/((Fs*w)-a+1j*b) # analytical
plt.figure(1)
plt.subplot(121)
plt.plot(w,np.real(Gn),'.--',label='numeric')
plt.plot(w,np.real(Gr),'.--',label='numeric reversed')
plt.plot(w,np.real(Ga),label='analytic')
plt.xlabel('freq, w')
plt.title('real part of FFT')
plt.legend(loc='best')
plt.xlim((-.02,.02))
plt.subplot(122)
plt.plot(w,np.imag(Gn),'.--',label='numeric')
plt.plot(w,np.imag(Gr),'.--',label='numeric reversed')
plt.plot(w,np.imag(Ga),label='analytic')
plt.xlabel('freq, w')
plt.title('imag part of FFT')
plt.legend(loc='best')
plt.xlim((-.02,.02))
plt.figure(2)
plt.plot(w,np.real(Gr-Gn),'.--',label='real')
plt.plot(w,np.imag(Gr-Gn),'.--',label='imag')
plt.xlabel(r'freq, $\omega$')
plt.title(r'difference between FFT (reversed) and analytic')
plt.legend()
plt.xlim((-.1,.1))
gn = Fs*ifftshift(ifft(fftshift(Ga))) # numerical ifft
gnr = gn[::-1] # reversed numerical result
plt.figure(3)
plt.subplot(121)
plt.plot(t,np.real(gn),'.--',label='numeric')
plt.plot(t,np.real(gnr),'.--',label='numeric reversed')
plt.plot(t,np.real(g),label='analytic')
plt.xlabel('time, t')
plt.title('real part of IFFT')
plt.legend(loc='best')
plt.xlim((-1,1))
plt.subplot(122)
plt.plot(t,np.imag(gn),'.--',label='numeric')
plt.plot(t,np.imag(gnr),'.--',label='numeric reversed')
plt.plot(t,np.imag(g),'-',label='analytic')
plt.xlabel('time, t')
plt.title('imag part of IFFT')
plt.legend(loc='best')
plt.xlim((-1,1))
plt.figure(4)
plt.plot(t,np.real(gnr-g),'.--',label='real')
plt.plot(t,np.imag(gnr-g),'.--',label='imag')
plt.xlabel(r'time, t')
plt.title(r'difference between IFFT (reversed) and analytic')
plt.legend()
plt.xlim((-.1,.1))