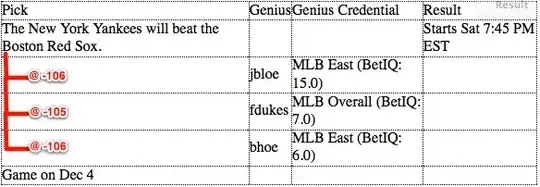
I'd like to understand the difference between an analytic and numeric FT of a function, using the numpy.fft module (i.e. why they are not the same). Starting with the equation
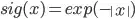 ,
,
the Fourier Transform of this can be shown to give an analytical FT (see e.g. Arfken, Weber and Harris p966, or sympy: fourier_transform(exp(-abs(x)), x, k) which is a factor of 2 * pi different):
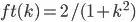 .
.
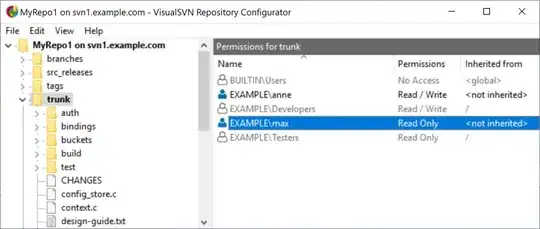
Using python/numpy to calculate the FFT of sig = np.exp(-np.abs(x)) gives a numerical FT that can plotted against the analytic solution (ft_numeric ~= ft_analytic x wave in plot).
The analytical FT can be seen to be a bounding window function for the numerical FT, and can be turned in to the numerical FT by multiplying by a suitable cos function (ft_analytic x wave overlaps ft_numeric, see example code for form of function).
My question is why does this numpy FFT produce a modified (modulated by a cos wave) numerical FT in this case? Is this to do with how the FFT is defined, and how can I tell this from its description: numpy FFT implementation.
import numpy as np
import numpy.fft as fft
import pylab as plt
x = np.linspace(-10, 10, 2001)
dx = x[1] - x[0]
normalization = 1 / dx
k = 2 * np.pi * fft.fftshift(fft.fftfreq(x.shape[0], d=dx))
# Signal.
sig = np.exp(-np.abs(x))
# Both shifted.
ft_numeric = fft.fftshift(fft.fft(sig))
ft_analytic = 2 / (1 + k**2)
wave = np.cos(2 * np.pi * k / (k[2] - k[0]))
plt.figure(1)
plt.clf()
plt.title('signal')
plt.plot(x, sig)
plt.xlabel('x')
plt.figure(2)
plt.clf()
plt.title('FT')
plt.plot(k, ft_analytic.real, label='ft_analytic')
plt.plot(k, normalization * ft_numeric, label='ft_numeric')
plt.plot(k, normalization * ft_numeric * wave, label='ft_analytic x wave')
plt.xlim((-15, 15))
plt.xlabel('k')
plt.legend()
plt.show()