1

Well, community:

Recently I have asked how to do exponential regression (Exponential regression function Python) thinking that for that data set the optimal regression was the Hyperbolic. 

x_data = np.arange(0, 51) 
y_data = np.array([0.001, 0.199, 0.394, 0.556, 0.797, 0.891, 1.171, 1.128, 1.437, 
          1.525, 1.720, 1.703, 1.895, 2.003, 2.108, 2.408, 2.424,2.537, 
          2.647, 2.740, 2.957, 2.58, 3.156, 3.051, 3.043, 3.353, 3.400, 
          3.606, 3.659, 3.671, 3.750, 3.827, 3.902, 3.976, 4.048, 4.018, 
          4.286, 4.353, 4.418, 4.382, 4.444, 4.485, 4.465, 4.600, 4.681, 
          4.737, 4.792, 4.845, 4.909, 4.919, 5.100])

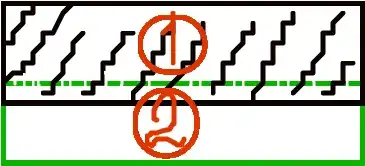
Now, I'm doubting:

Exponential

Hyperbolic

The first is an exponential fit. The second is hyperbolic. I don't know which is better... How to determine? Which criteria should I follow? Is there some python function?

Thanks in advance!

alienflow
  • 400
  • 7
  • 19
  • 5
    This is more of a math question rather than a programming question. One way to to compute the [MSE](https://en.wikipedia.org/wiki/Mean_squared_error) of both curves, and pick the one with the lower one. See more on [goodness of fit](https://en.wikipedia.org/wiki/Goodness_of_fit), [`scipy.metrics.mean_squared_error`](http://scikit-learn.org/stable/modules/generated/sklearn.metrics.mean_squared_error.html), [Mean Squared Error in numpy](https://stackoverflow.com/questions/16774849/mean-squared-error-in-numpy). – pault Jun 06 '18 at 16:28
  • Do your data points have error bars? If so, are they gaussian errors? – user545424 Jun 06 '18 at 16:52

3 Answers3

2

One common fit statistic is R-squared (R2), which can be calculated as "R2 = 1.0 - (absolute_error_variance / dependent_data_variance)" and it tells you what fraction of the dependent data variance is explained by your model. For example, if the R-squared value is 0.95 then your model explains 95% of the dependent data variance. Since you are using numpy, the R-squared value is trivially calculated as "R2 = 1.0 - (abs_err.var() / dep_data.var())" since numpy arrays have a var() method to calculate variance. When fitting your data to the Michaelis-Menten equation "y = ax / (b + x)" with parameter values of a = 1.0232217656373191E+01 and b = 5.2016057362771100E+01 I calculate an R-squared value of 0.9967, which means that 99.67 percent of the variance in the "y" data is explained by this model. Howver, there is no silver bullet and it is always good to verify other fit statistics and visually inspect the model. Here is my plot for the example I used: model.png

James Phillips
  • 4,526
  • 3
  • 13
  • 11
1

Well, you should calculate an error function which measures how good your fit actually is. There are many different error functions you could use but for the start the mean-squared-error should work (if you're interested in further metrics, have a look at http://scikit-learn.org/stable/modules/model_evaluation.html).

You can manually implement mean-squared-error, once you determined the coefficients for your regression problem:

from sklearn.metrics import mean_squared_error
f = lambda x: a * np.exp(b * x) + c 
mse = mean_squared_error(y_data, f(x_data))
pythonic833
  • 3,054
  • 1
  • 12
  • 27
1

You can take the 2-norm between the function and line of fit. Python has the function np.linalg.norm The R squared value is for linear regression.

  • My understanding is R-squared is exact for linear regression and approximate for non-linear regression. Still useful as it has no units, making comparisons of different data set regressions easier. For example, an R-squared value of 0.5 when fitting data with units of light-years and an R-squared value of 0.99 when fitting data with units of milliliters does give an understanding of the fit quality in both cases. – James Phillips Jun 06 '18 at 17:46
  • 1
    That is my understanding as well –  Jun 06 '18 at 17:48