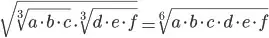Resampling a time series to year to date

Question

Let's say I'm looking at the US Treasury bill maturity data. It's measured daily, but not really daily, as a per cent rate.

I can get the geometric mean of a quarter's rate like so:

import pandas as pd
from scipy.stats.mstats import gmean
# ...
tbill_quarterly = raw_tbill.resample('Q').apply(lambda x: gmean(x).item())

How would I get a year-to-date quarterly aggregate from this data? That is, a figure each quarter (for 2018: 2018-03-31, 2018-06-30, 2018-09-30, 2018-12-31) holding the return from the start of the year to the quarterly date.

The resampling documentation (or really, the StackOverflow answer which serves as replacement for non-existent documentation) only provides frequencies. And I can't seem to find some kind of year-to-date function in scipy.stats.

Answer 1

I hate to post an answer to my own question, but having solved the problem, I feel that I should, in the case that someone else comes on a problem like this. I don't guarantee that this is the most elegant solution. It probably isn't.

I downloaded the data from FRED (link in answer) into a file treasury-1year-rates_1980-present.csv containing the data from the 1979-12-31 point to present (currently 2018-06-12). You need to get the data point for 1979-12-31 because 1980-01-01 is NA, since that is a federal holiday, being the New Year.

raw_tbill = pd.read_csv(path.join(base_dir, 'treasury-1year-rates_1980-present.csv'),
                        parse_dates=['DATE'], na_values=['.'])
raw_tbill.columns = [s.lower() for s in raw_tbill.columns.values.tolist()]
print(f'Loaded t-bill 1-year rates data, from 1980 to present, with {len(raw_tbill)} entries')

The FRED data uses . to representing missing data. Thus, the inclusion of na_values['.'] and we also want the date column parsed, thus, the inclusion of the parse_dates parameter.

I happen to like to have everything in lower case. It's only kept here because I don't want to change all the following column names. That's a real pain.

Two misconceptions, or gotcha's, to get out of the way first.

Arithmetic means wrong. Arithmetic means are wrong for dealing with per cent data. You should be using geometric means. See this for more clarification. This creates the quarter by quarter data.

Data not actually daily. Anyway, this data isn't actually daily. To deal with that problem, and the fact that Treasury bills still pay on holidays and weekends, all of those weekends need to be filled in with forward propagated data. Otherwise, the geometric means will be wrong, since one of the geometric mean assumptions is that the data are evenly spaced in time (unless you weight them, which is effectively the same thing that I do here, but I did this because calculating weights takes time to think through. This doesn't).

# fill in days and put in the previous applicable figure
# need to deal with gaps in data
raw_tbill.set_index('date', inplace=True)
raw_tbill.dropna(inplace=True)
tbill_data = raw_tbill.reindex(pd.date_range(raw_tbill.index.min(), raw_tbill.index.max(), freq='D'),
                               method='ffill')

Years not complete. After completing this, I have years that aren't actually really filled in (for example, apparently 1979-12-31 is empty). They need to be removed for being useless.

# drop incomplete years
count = tbill_data.set_index([tbill_data.index.year, tbill_data.index.day]).count(level=0)
years = count[count['dgs1'] >= 365].index
tbill_data['tmp_remove'] = tbill_data.apply(lambda r : 0 if r.name.year in years else 1, axis=1)
tbill_data = tbill_data[tbill_data['tmp_remove'] == 0].drop('tmp_remove', axis=1)

From here, if you're following the code, the index is now DatetimeIndex. Thus, there is no date column.

Get quarter indices and calculate. Now, technically, you don't need to do this step. It's in my code because I have to produce it. In this processing path, you have to do it, however, just to get the indices for each quarter. Otherwise, no quarters, no cigar.

Also, the DSG1 data is in per cent, we don't want those, if you're doing anything with it, you probably want it in a proportion, ie 100 pc = 1.

# turn the daily tbill data into quarterly data
# use geometric means
tbill_data['dgs1'] = tbill_data['dgs1'] / 100
tbill_qtrly = tbill_data.resample('Q').apply(lambda x: gmean(x).item())

Anyway I then define a function to calculate the year to date, which also uses geometric means for this. This then subsets the relevant data to the date. I believe that year to date includes the report date, justifying <=. If it doesn't actually do that, comment.

def calculate_ytd(row):
    year = row.name.year
    year_data = tbill_data[tbill_data.index.year == year]
    applicable_data = year_data[year_data.index <= row.name]
    return gmean(applicable_data['dgs1'])

tbill_qtrly['dgs1_ytd'] = tbill_qtrly.apply(lambda r : calculate_ytd(r), axis=1)

Application of that function produces the data.

Post-script. One could also use the quarterly geometric means as a basis for calculation, if all input variables are positive, since

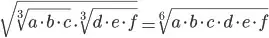
where all the variables a through e are positive.

Answer 2

Using help from Pandas DataFrame groupby overlapping intervals of variable length

import pandas as pd
import numpy as np
from scipy.stats.mstats import gmean


# Get data & format
df = pd.read_csv("...\DGS1.csv")
def convert(x):
    try:
        return float(x)
    except ValueError:
        return np.nan

# Format data
df['DATE'] = pd.to_datetime(df.DATE)
df['DGS1'] = df.DGS1.map(convert)
df = df.set_index('DATE').dropna()

# Reindex date according to @ifly6 answer
df = df.reindex(pd.date_range(df.index.min(), df.index.max(), freq='D'),method='ffill')
df = df.reset_index().rename(columns={'index': 'date'})

# Determine if the date sits inside the date interval
def year_to_quarter_groups(x):
    return pd.Series([l for l in bins if l[0] <= x <= l[1]])

# Create all the date intervals
# bins = [
#     (pd.datetime(2013, 1, 1), pd.datetime(2013, 3, 31)),  
#     (pd.datetime(2013, 1, 1), pd.datetime(2013, 6, 30)),
#     ...
# ]
dates_from_ = [[i]*4 for i in  pd.date_range('1/1/2013', end='1/1/2019', freq='AS')]
dates_from = [item for sublist in dates_from_ for item in sublist]  # flatten list
dates_to = pd.date_range('1/1/2013', end='1/1/2019', freq='Q')
bins = list(zip(dates_from, dates_to))

# Create a set of intervals that each date belongs to
# A date can belong to up to four intervals/quarters [0, 1, 2, 3]
intervals = df['date'].apply(year_to_quarter_groups).stack().reset_index(1, drop=True)

# Combine the dataframes
new = pd.concat([df, intervals], axis=1).rename(columns={0: 'year_to_quarter'}).drop('date', axis=1)

# Calculate the geometric mean
new.groupby(['year_to_quarter']).DGS1.apply(lambda x: gmean(x))

Out[]:
year_to_quarter
(2013-01-01 00:00:00, 2013-06-30 00:00:00)    0.140469
(2013-01-01 00:00:00, 2013-09-30 00:00:00)    0.125079
(2013-01-01 00:00:00, 2013-12-31 00:00:00)    0.124699
(2014-01-01 00:00:00, 2014-03-31 00:00:00)    0.119801
(2014-01-01 00:00:00, 2014-06-30 00:00:00)    0.110655
(2014-01-01 00:00:00, 2014-09-30 00:00:00)    0.109624
(2014-01-01 00:00:00, 2014-12-31 00:00:00)    0.117386
(2015-01-01 00:00:00, 2015-03-31 00:00:00)    0.222842
(2015-01-01 00:00:00, 2015-06-30 00:00:00)    0.235393
(2015-01-01 00:00:00, 2015-09-30 00:00:00)    0.267067
(2015-01-01 00:00:00, 2015-12-31 00:00:00)    0.301378
(2016-01-01 00:00:00, 2016-03-31 00:00:00)    0.574620
(2016-01-01 00:00:00, 2016-06-30 00:00:00)    0.569675
(2016-01-01 00:00:00, 2016-09-30 00:00:00)    0.564723
(2016-01-01 00:00:00, 2016-12-31 00:00:00)    0.605566
(2017-01-01 00:00:00, 2017-03-31 00:00:00)    0.882396
(2017-01-01 00:00:00, 2017-06-30 00:00:00)    0.994391
(2017-01-01 00:00:00, 2017-09-30 00:00:00)    1.071789
(2017-01-01 00:00:00, 2017-12-31 00:00:00)    1.175368
(2018-01-01 00:00:00, 2018-03-31 00:00:00)    1.935798
(2018-01-01 00:00:00, 2018-06-30 00:00:00)    2.054127
(2018-01-01 00:00:00, 2018-09-30 00:00:00)    2.054127
(2018-01-01 00:00:00, 2018-12-31 00:00:00)    2.054127