2

Inspired by this question, the asker assumes that the users of a system would very rarely take some action at the exact same time as each other.

Given what I know of making assumptions like that I can guarantee that users would infact do things at the same time. However, I am at a loss as to how you would actually calculate the expected frequency of collisions.

E.g. If we assume each user is taking an action every 3 minutes and our timer is really only accurate to the millisecond, what is the formula for calculating the frequency of collisions?

Given the Wikipedia entry for the birthday problem can be generalised into the formula 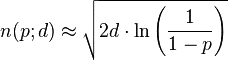Birthday problem Where d is the 180,000 milliseconds and p the probability of a collision.

So with 3 users say, we get a probability of 2.4996E-05 in any given 3 minute period that there is a collision.

The issue then becomes what are the chances of a collision during the day? There being 60-*60*8/3 = 9600 3 minute periods in the working day, the probability of a collision in any given day then be comes 1-((1-2.4996E-05)^9600) = 21%. A pretty good chance of things going pear shaped.

Community
  • 1
  • 1
Nat
  • 14,175
  • 5
  • 41
  • 64
  • Try http://math.stackexchange.com/ - you're asking for a formula, & this really has nothing to do with programming. – Kirk Broadhurst Feb 23 '11 at 03:23
  • or [stats.stackexchange.com](http://stats.stackexchange.com/questions/1308/extending-the-birthday-paradox-to-more-than-2-people) even – Nat Feb 23 '11 at 04:02
  • 1
    The fact that you think this has nothing to do with programming is kind of depressing. The fact that your opinion is widely shared is one reason so many systems have such performance problems. – Charlie Martin Feb 23 '11 at 15:47

5 Answers5

2

In 3 minutes you will have 180000 milliseconds. If you know the number of users, you can use the probability of the Birthday Paradox to determine the odds of a collision.

Consider too that your timer might not be accurate to the millisecond, even though it might be measured in milliseconds. Many timers are based on a tick that runs much less than 1000 times a second.

Mark Ransom
  • 299,747
  • 42
  • 398
  • 622
1

3 minutes = 180 seconds = 180000. Call this M for milliseconds.

How many users do you have? Let's say there's N.

In a 3 minute time period, user 1 gobbles up a millisecond - a 180000 free, 180000 possible - that's 180000/180000 = 1 chance to succeed.

Next guy: 179999 / 180000 chance to get a good slot. Next guy: 179998 / 180000 chance to get a good slot.

The chances of all of those is

 180000 * 179999 * 179998 . . .
--------------------------------
 180000 * 180000 * 180000 . . .

In short:

 N! / ((N^N)*(N-M)!)
corsiKa
  • 81,495
  • 25
  • 153
  • 204
1

The to get the frequency of collisions, just get the probability of a collision during a 1 mS interval, then scale up to whatever interval you like (e.g. multiply by 1000 to get collisions per second).

To get that probability, get the probability of no collision during a 1 mS time interval? That's the probability that the number of users acting during that interval is 1 or 0.

If there are n users, and the probability of a particular user acting during the time interval is p, then

P(0) = (1-p)n = 1 - np + n(n-1)p2/2 - ...
P(1) = np(1-p)n-1 = np - n(n-1)p2 + ...
P(0 or 1) = 1 - n(n-1)p2/2 + ...
P(more than 1) = n(n-1)p2/2 + ...

Now to plug in some numbers: once every 3 minutes gives p=1.8x10-5, so the probability of collision is approximately

n(n-1)(3.24x10-10)

So if my calculations are correct, if you have 100 users, you'll get roughly one collision every ten minutes.

Beta
  • 96,650
  • 16
  • 149
  • 150
0

The key thing for this question is knowing the probability of an event happening in an interval, and knowing how long the event takes to complete. Then the probability for both will be the probability of the second event happening during the duration of the firrst event, conditioned on the probability of the first event.

Now you can compute this, in general, based on Bayes Rule.

Charlie Martin
  • 110,348
  • 25
  • 193
  • 263
  • Given the interval in the example is 3min and the duration is 1 ms, how do you calculate this specifically? Particularly, how do you create a formula when given X users with the above behaviour? – Nat Feb 23 '11 at 03:23
0

CollisionFreqPercent = ( AccuracySecs / ( ActionDelaySecs / ConcurrentUsers ) ) * 100;

eg:

1 user= ( 0.001 / ( ( 3 * 60 ) / 1 ) ) * 100 = 0.00055% chance of collision at any given time

1000 users= ( 0.001 / ( ( 3 * 60 ) / 1000 ) ) * 100 = 0.55% chance of collision at any given time

servermanfail
  • 2,532
  • 20
  • 21