Algorithm for Finding Redundant Edges in a Graph or Tree

Question

Is there an established algorithm for finding redundant edges in a graph?

For example, I'd like to find that a->d and a->e are redundant, and then get rid of them, like this:

=>

Edit: Strilanc was nice enough to read my mind for me. "Redundant" was too strong of a word, since in the example above, neither a->b or a->c is considered redundant, but a->d is.

Answer 1

You want to compute the smallest graph which maintains vertex reachability.

This is called the transitive reduction of a graph. The wikipedia article should get you started down the right road.

Answer 2

Since the Wikipedia article mentioned by @Craig gives only a hit for an implementation, I post my implementation with Java 8 streams:

Map<String, Set<String>> reduction = usages.entrySet().stream()
                .collect(toMap(
                        Entry::getKey,
                        (Entry<String, Set<String>> entry) -> {
                            String start = entry.getKey();
                            Set<String> neighbours = entry.getValue();
                            Set<String> visited = new HashSet<>();
                            Queue<String> queue = new LinkedList<>(neighbours);

                            while (!queue.isEmpty()) {
                                String node = queue.remove();
                                usages.getOrDefault(node, emptySet()).forEach(next -> {
                                    if (next.equals(start)) {
                                        throw new RuntimeException("Cycle detected!");
                                    }
                                    if (visited.add(next)) {
                                        queue.add(next);
                                    }
                                });
                            }

                            return neighbours.stream()
                                    .filter(s -> !visited.contains(s))
                                    .collect(toSet());
                        }
                ));

Answer 3

Several ways to attack this, but first you're going to need to define the problem a little more precisely. First, the graph you have here is acyclic and directed: will this always be true?

Next, you need to define what you mean by a "redundant edge". In this case, you start with a graph which has two paths a->c: one via b and one direct one. From this I infer that by "redundant" you mean something like this. Let G=< V, E > be a graph, with V the set of vertices and E ⊆ V×V the set of edges. It kinda looks like you're defining all edges from v_i to v_j shorter than the longest edge as "redundant". So the easiest thing would be to use depth first search, enumerate the paths, and when you find a new one that's longer, save it as the best candidate.

I can't imagine what you want it for, though. Can you tell?

Answer 4

I think the easiest way to do that, actually imagine how it would look in the real work, imagine if you have joints, Like

(A->B)(B->C)(A->C), imagine if distance between near graphs is equals 1, so

(A->B) = 1, (B->C) = 1, (A->C) = 2.

So you can remove joint (A->C).

In other words, minimize.

This is just my idea how I would think about it at start. There are various articles and sources on the net, you can look at them and go deeper.

Resources, that Will help you:

Algorithm for Removing Redundant Edges in the Dual Graph of a Non-Binary CSP

Graph Data Structure and Basic Graph Algorithms

Google Books, On finding minimal two connected Subgraphs

Graph Reduction

Redundant trees for preplanned recovery in arbitraryvertex-redundant or edge-redundant graphs

Answer 5

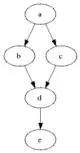
I had a similar problem and ended up solving it this way:

My data structure is made of dependends dictionary, from a node id to a list of nodes that depend on it (ie. its followers in the DAG). Note it works only for a DAG - that is directed, acyclic graph.

I haven't calculated the exact complexity of it, but it swallowed my graph of several thousands in a split second.

_transitive_closure_cache = {}
def transitive_closure(self, node_id):
    """returns a set of all the nodes (ids) reachable from given node(_id)"""
    global _transitive_closure_cache
    if node_id in _transitive_closure_cache:
        return _transitive_closure_cache[node_id]
    c = set(d.id for d in dependents[node_id])
    for d in dependents[node_id]:
        c.update(transitive_closure(d.id))  # for the non-pythonists - update is update self to Union result
    _transitive_closure_cache[node_id] = c
    return c

def can_reduce(self, source_id, dest_id):
    """returns True if the edge (source_id, dest_id) is redundant (can reach from source_id to dest_id without it)"""
    for d in dependents[source_id]:
        if d.id == dest_id:
            continue
        if dest_id in transitive_closure(d.id):
            return True # the dest node can be reached in a less direct path, then this link is redundant
    return False

# Reduce redundant edges:
for node in nodes:      
    dependents[node.id] = [d for d in dependents[node.id] if not can_reduce(node.id, d.id)]