I am just curious to know, how does PyTorch track operations on tensors (after the .requires_grad is set as True and how does it later calculate the gradients automatically. Please help me understand the idea behind autograd. Thanks.
- 700
- 1
- 9
- 18
1 Answers
That's a great question!
Generally, the idea of automatic differentiation (AutoDiff) is based on the multivariable chain rule, i.e.
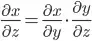 .
.
What this means is that you can express the derivative of x with respect to z via a "proxy" variable y; in fact, that allows you to break up almost any operation in a bunch of simpler (or atomic) operations that can then be "chained" together.
Now, what AutoDiff packages like Autograd do, is simply to store the derivative of such an atomic operation block, e.g., a division, multiplication, etc.
Then, at runtime, your provided forward pass formula (consisting of multiple of these blocks) can be easily turned into an exact derivative. Likewise, you can also provide derivatives for your own operations, should you think AutoDiff does not exactly do what you want it to.
The advantage of AutoDiff over derivative approximations like finite differences is simply that this is an exact solution.
If you are further interested in how it works internally, I highly recommend the AutoDidact project, which aims to simplify the internals of an automatic differentiator, since there is usually also a lot of code optimization involved. Also, this set of slides from a lecture I took was really helpful in understanding.
- 700
- 1
- 9
- 18
- 9,890
- 1
- 42
- 63
-
1thanks a lot for the explanation, what you want to say is AutoDIff converts our forward pass into some kind of Gradient Flow graph that consists of atomic operations like addition and multiplication, and then use the atomic differentiation with chain rule to find the differentiation of whole forward pass, right? – NoSuchUserException Jun 27 '18 at 09:50
-
Exactly! I forgot to mention this explicitly, but indeed AutoDiff builds a graph that is then iterated through. Note that the multivariable chain rule has some more details that are also covered by the graph, but not mentioned in the answer (specifically if you have mulitple paths from x to z, say via two different variables y1 and y2. Then, your derivative would be: dx/dz = dx/dy1*dy1/dz + dx/dy2*dy2/dz. – dennlinger Jun 27 '18 at 10:23