Improvement of performance for a maze solving program in Python

Question

fellow programmers. I need help with one of my projects. I'm making a maze solving program. It reads an image file, which has to be black and white (black pixels are walls, white pixels are paths), have only one pixel at the top which is the entrance to the maze, and only one white pixel at the bottom which is the exit.

There're three main parts to the code:

1) The program first create nodes in the maze, respecting a set of rules. For exemple here's a simple maze:

and here're all the nodes drawn in red:

The nodes are like the corners, the crossroads, every point where you can change direction. The distance between each node and the exit of the maze is also measured. While it's generating all the nodes, it places them in a list.

2) As soon as all the nodes are generated, the program will iterate through all the nodes in the list, and try to search in every direction possible for other nodes, to "link" them, establish the possible paths. For exemple, if it detects that there is a path above a node, it'll search each and every pixel in a line from the coordinate of the node, and going up, iterating through ALL of the node list again to see if another node match these coordinates. If it finds one at some point, it links them, and start searching to the right (if there's a path to the right of course), and etc for every direction.

3) Once all of the nodes are linked together and every possible paths established, it's gonna start from the entry node of the maze, and run my implementation of the A* algorithm to figure out the right path, and go back if it's in a dead end. As you can see, it solves mazes without difficulty.

So my program works. What's the problem then? The problem is the node linking part. On small mazes, it takes like half a second. But make the maze somewhat bigger, then the number of nodes will drastically increase. And since it iterates through the node list A LOT of time (one time for every pixel it searches for every node), you can imagine if I have 600 000 nodes... It's gonna take ages.

So that's what I'm asking help for: a better, faster way to link the nodes together. I've posted the entire code on pastebin (https://pastebin.com/xtmTm7wb, sorry if it's a little messy, it was VERY late when I programmed this). The node linking part starts at line 133 and ends at line 196.

Here's the node linking code:

counter = 0
last = 0
for node in nodelist:
    a = node.pos[0]
    b = node.pos[1]
    if node.paths[0]:
        for i in range(b-1,0,-1):
            if mazepix[a,i] == blackpix:
                break
            if any(x.pos == (a,i) for x in nodelist):
                for iteration in nodelist:
                    if iteration.pos == (a,i):
                        indexofnodetolinkto = iteration.index
                        break
                node.connections.append(indexofnodetolinkto)
                # print("Linking node %d and node %d..."%(node.index, indexofnodetolinkto))
                break

    if node.paths[1]:
        for i in range(a+1,maze.size[0]):
            if mazepix[i,b] == blackpix:
                break
            if any(x.pos == (i,b) for x in nodelist):
                for iteration in nodelist:
                    if iteration.pos == (i,b):
                        indexofnodetolinkto = iteration.index
                        break
                node.connections.append(indexofnodetolinkto)
                # print("Linking node %d and node %d..."%(node.index, indexofnodetolinkto))
                break

    if node.paths[2]:
        for i in range(b+1,maze.size[1]):
            if mazepix[a,i] == blackpix:
                break
            if any(x.pos == (a,i) for x in nodelist):
                for iteration in nodelist:
                    if iteration.pos == (a,i):
                        indexofnodetolinkto = iteration.index
                        break
                node.connections.append(indexofnodetolinkto)
                # print("Linking node %d and node %d..."%(node.index, indexofnodetolinkto))
                break

    if node.paths[3]:
        for i in range(a-1,0,-1):
            if mazepix[i,b] == blackpix:
                break
            if any(x.pos == (i,b) for x in nodelist):
                for iteration in nodelist:
                    if iteration.pos == (i,b):
                        indexofnodetolinkto = iteration.index
                        break
                node.connections.append(indexofnodetolinkto)
                # print("Linking node %d and node %d..."%(node.index, indexofnodetolinkto))
                break

    counter += 1
    percent = (counter/nbrofnodes)*100
    if int(percent)%10 == 0 and int(percent) != last:
        print("Linking %d%% done..."%percent)
        last = int(percent)

print("All node linked.")

Thank you if you read all of this, I know it's not a very precise question, but I've spend so much time trying to make this work, now that it does I'm really stuck on the ways I could improve it ^^'.

Answer 1

Your program is super slow, because this part takes a long time and you do it many times for every node:

            for iteration in nodelist:
                if iteration.pos == (i,b):
                    indexofnodetolinkto = iteration.index
                    break

There are a lot of ways to make it a lot faster.

You could put the nodes into a dictionary using the position as a key, so you can just do a lookup for a position to find the node there.

Even better, you could put the nodes into row lists and column lists, sorted by position, and then only try to connect adjacent nodes in the lists.

But the best thing to do is to forget about these nodes altogether and just do a BFS search directly on the bitmap.

Since this is a fun problem, I wrote a fast version with a simple BFS. I don't want to ruin all your fun, so here's just the BFS part so that you can see what I mean by doing BFS directly on the image:

#Breadth-first search over the graph
#We use special colored pixels in the image to mark visited locations and their distance
nextlevel=[(entrypos,0)]
nextdist=0
mazepix[entrypos,0] = markerPixel(nextdist)
exitpos = -1
while exitpos<0:
    if len(nextlevel) < 1:
        print("Could not find exit!")
        return
    prevlevel = nextlevel
    nextdist += 1
    nextlevel = []
    nextpix = markerPixel(nextdist)

    for prevpos in prevlevel:
        for dir in [(-1,0),(0,1),(1,0),(0,-1)]:
            x = prevpos[0]+dir[0]
            y = prevpos[1]+dir[1]
            if x>=0 and y>=0 and x<W and y<H and mazepix[x,y]==whitepix:
                nextlevel.append((x,y))
                #mark it used and distance mod 3
                mazepix[x,y]=nextpix
                if y>=H-1:
                    exitpos=x

Instead of using a separate set with objects and links to remember the path, we mark pixels as visited directly in the image. Instead of using actual links of any kind to link one pixel to another, we just check all 4 directions looking for adjacent white pixels whenever we need to.

This does a level-by-level BFS so we always know how far new pixels are from the entrance, and the color we mark a visited pixel indicates its distance from the entrance (mod 3). This allows us to reconstruct the shortest path when we find the exit.

EDIT: It's been a long time and the OP has had his fun, so here's the complete python solver:

from PIL import Image
import math
import sys
import time
import pickle
import os

whitepix = (255,255,255)
blackpix = (0,0,0)
redpix = (255,0,0)
greenpix = (0,255,0)

def markerPixel(distance):
    val=120+(distance%3)*40
    return (val,val,0)

def smallerMarker(pixel):
    return markerPixel(pixel[0]-1)

def isMarker(pixel):
    return pixel[2]==0 and pixel[0]==pixel[1] and pixel[0]>=120

def solve(imagename, outputname, showmarkers):

    maze = Image.open(imagename)
    maze = maze.convert('RGB')
    mazepix = maze.load()
    nodelist = []

    print(maze.size)

    starttime = time.time()

    W = maze.size[0]
    H = maze.size[1]
    entrypos = -1

    # Find the entry
    for i in range(0,W):
        if mazepix[i, 0] == whitepix:
            entrypos=i
            break

    if entrypos < 0:
        print("No entry!")
        return

    #Breadth-first search over the graph
    #We use special colored pixels in the image to mark visited locations and their distance
    nextlevel=[(entrypos,0)]
    nextdist=0
    mazepix[entrypos,0] = markerPixel(nextdist)
    exitpos = -1
    while exitpos<0:
        if len(nextlevel) < 1:
            print("Could not find exit!")
            return
        prevlevel = nextlevel
        nextdist += 1
        nextlevel = []
        nextpix = markerPixel(nextdist)

        for prevpos in prevlevel:
            for dir in [(-1,0),(0,1),(1,0),(0,-1)]:
                x = prevpos[0]+dir[0]
                y = prevpos[1]+dir[1]
                if x>=0 and y>=0 and x<W and y<H and mazepix[x,y]==whitepix:
                    nextlevel.append((x,y))
                    #mark it used and distance mod 3
                    mazepix[x,y]=nextpix
                    if y>=H-1:
                        exitpos=x

    #found the exit -- color the path green
    nextpos = (exitpos,H-1)
    while nextpos != None:
        nextpix = smallerMarker(mazepix[nextpos[0],nextpos[1]])
        prevpos = nextpos
        mazepix[nextpos[0],nextpos[1]] = greenpix
        nextpos = None
        #find the next closest position -- all adjacent positions are either
        #1 closer, 1 farther, or the same distance, so distance%3 is enough
        #to distinguish them
        for dir in [(-1,0),(0,1),(1,0),(0,-1)]:
            x = prevpos[0]+dir[0]
            y = prevpos[1]+dir[1]
            if x>=0 and y>=0 and x<W and y<H and mazepix[x,y]==nextpix:
                nextpos=(x,y)
                break

    #Erase the marker pixels if desired
    if not showmarkers:
        for y in range(0,H):
            for x in range(0,W):
                if isMarker(mazepix[x,y]):
                    mazepix[x,y]=whitepix

    maze.save(outputname)

solve("maze.gif", "solved.png", False)

Answer 2

Your maze is just 301x301 pixels so in my opinion 0.5 seconds is too big time for the solution. When I used raster A* approach:

• How to speed up A* algorithm at large spatial scales?

The whole solution took just ~1.873ms which is huge difference to yours ~500ms. Of coarse graph A* has bigger overhead so I was curious and wanted to test it so I encoded mine version (in C++ based on the same code as in the link above) and the result was that graph acquisition from image took up to ~3ms and graph A* took up to ~0.18ms so still huge difference with yours (+/- computer setup difference).

So what to check for first?

I am no python coder but I do not see any image access in your code. You should check if your image access is fast or not. That is common mistake for rookies using stuff like

GetPixel/PutPixel
Pixels[][]

Those are usually painfully slow (in my experience on GDI Win32 like 1000-10000 times slower than direct pixel access) and make a huge difference if corrected. for more info see:

• Display an array of color in C

Another usual mistake with lists usage is to incrementally adding element to list without preallocation. For small list its not a problem but with large number of elements the reallocation in case of adding element slows things down by copying the stuff over and over again. The same goes for inserting and deleting element in lists. Improving list access make huge impact especially for polynomial complexities like O(n^2) and slower...

Algorithm

Small changes in algorithm can do a huge impact. In your case I used combination of DIP edge detecting techniques and accelerating structures for topologically sorted edges. That changes the O(n) or O(n^2) searches to simple O(1) operations. The idea is to have ordered list of all vertexes of maze sorted by xy and yx. If each vertex knows its index in such structure it can easily obtain its neighbor vertexes...

Stack/heap trashing

this slows things down a lot. Especially with recursive functions. The bigger recursion level and operands size passed the worse the effect.

Here my simple C++ example based on the link above

//---------------------------------------------------------------------------
//--- A star class ver: 1.00 ------------------------------------------------
//---------------------------------------------------------------------------
#ifndef _A_star_h
#define _A_star_h
//---------------------------------------------------------------------------
#include "list.h"
//---------------------------------------------------------------------------
class A_star_graph
    {
public:
    // variables
    struct _pnt
        {
        int x,y;            // 2D position (image)
        int mx;             // mxy[y][mx] index
        int my;             // mxy[x][my] index
        int pN,pS,pE,pW;    // index of linked point in direction or -1
        int lN,lS,lE,lW;    // distance to linked point in direction or 0 (cost for A*)
        int a;              // value for A*
        _pnt()  {}
        _pnt(_pnt& a)   { *this=a; }
        ~_pnt() {}
        _pnt* operator = (const _pnt *a) { *this=*a; return this; }
        //_pnt* operator = (const _pnt &a) { ...copy... return this; }
        };
    List<_pnt> pnt;         // list of all vertexes
    List< List<int> > mxy,myx;  // xy and yx index sorted pnt[] (indexes of points)
    List<int>  path;        // found path (indexes of points)

    int xs,ys;              // map esolution
    DWORD col_space;        // colors for rendering
    DWORD col_wall ;
    DWORD col_path ;

    // internals
    A_star_graph();
    A_star_graph(A_star_graph& a)   { *this=a; }
    ~A_star_graph(){}
    A_star_graph* operator = (const A_star_graph *a) { *this=*a; return this; }
    //A_star_graph* operator = (const A_star_graph &a) { ...copy... return this; }

    // inteface
    void reset();                                       // clear all
    void ld(Graphics::TBitmap *bmp,DWORD col_wall);     // create graph from bitmap col_wall is 0x00RRGGBB
    void draw(Graphics::TBitmap *bmp);                  // draw map to bitmap for debuging
    void compute(int p0,int p1);                        // compute path from pnt[p0] to pnt[p1] into path[]
    };
//---------------------------------------------------------------------------
A_star_graph::A_star_graph()
    {           //BBGGRR
    col_space=0x00FFFFFF;
    col_wall =0x00000000;
    col_path =0x00FFAA40;
    reset();
    }
//---------------------------------------------------------------------------
void A_star_graph::reset()
    {
    int x,y; xs=0; ys=0; pnt.num=0; path.num=0;
    for (x=0;x<mxy.num;x++) mxy[x].num=0; mxy.num=0;
    for (y=0;y<myx.num;y++) myx[y].num=0; myx.num=0;
    }
//---------------------------------------------------------------------------
void A_star_graph::ld(Graphics::TBitmap *bmp,DWORD col_wall)
    {
    _pnt p,*pp,*qq;
    int i,j,x,y,c[10]={0,0,0,0,0,0,0,0,0,0};
    DWORD *p0,*p1,*p2;
    reset();
    xs=bmp->Width;
    ys=bmp->Height;
    mxy.allocate(xs); mxy.num=xs; for (x=0;x<xs;x++) mxy[x].num=0;
    myx.allocate(ys); myx.num=ys; for (y=0;y<ys;y++) myx[y].num=0;
    if (!ys) return;
    p.pN=-1; p.pS=-1; p.pE=-1; p.pW=-1; p.mx=-1; p.my=-1;
    p0=NULL; p1=NULL; p2=(DWORD*)bmp->ScanLine[0];
    for (p.y=0;p.y<ys;p.y++)
        {
        p0=p1; p1=p2; p2=NULL;
        if (p.y+1<ys) p2=(DWORD*)bmp->ScanLine[p.y+1];
        for (p.x=0;p.x<xs;p.x++)
         if ((p1[p.x]&0x00FFFFFF)!=col_wall)    // ignore wall pixels
            {
            // init connection info
            p.lN=0; p.lS=0; p.lE=0; p.lW=0;
            // init c[] array with not a wall predicates for 4-neighbors
            c[2]=0; c[4]=0; c[5]=1; c[6]=0; c[8]=0;
            if (p0) if ((p0[p.x]&0x00FFFFFF)!=col_wall) c[8]=1;
            if (p2) if ((p2[p.x]&0x00FFFFFF)!=col_wall) c[2]=1;
            if (p1)
                {
                if (p.x-1> 0) if ((p1[p.x-1]&0x00FFFFFF)!=col_wall) c[4]=1;
                if (p.x+1<xs) if ((p1[p.x+1]&0x00FFFFFF)!=col_wall) c[6]=1;
                }
            // detect vertex and its connection
            i=0;
            if (( c[2])&&(!c[8])){ i=1; p.lS=1; }   // L
            if ((!c[2])&&( c[8])){ i=1; p.lN=1; }
            if (( c[4])&&(!c[6])){ i=1; p.lW=1; }
            if ((!c[4])&&( c[6])){ i=1; p.lE=1; }
            j=c[2]+c[4]+c[6]+c[8];
            if (j==3)               // T
                {
                i=1; p.lN=1; p.lS=1; p.lW=1; p.lE=1;
                if (!c[2]) p.lS=0;
                if (!c[8]) p.lN=0;
                if (!c[6]) p.lE=0;
                if (!c[4]) p.lW=0;
                }
            if (j==4)               // +
                {
                i=1; p.lN=1; p.lS=1; p.lW=1; p.lE=1;
                }
            // add point
            if (i)
                {
                p.mx=myx[p.y].num;
                p.my=mxy[p.x].num;
                mxy[p.x].add(pnt.num);
                myx[p.y].add(pnt.num);
                pnt.add(p);
                }
            }
        }
    // find connection between points
    for (pp=pnt.dat,i=0;i<pnt.num;i++,pp++)
        {
        if (pp->lE)
            {
            j=myx[pp->y][pp->mx+1]; qq=pnt.dat+j; pp->pE=j; qq->pW=i;
            j=abs(qq->x-pp->x)+abs(qq->y-pp->y);  pp->lE=j; qq->lW=j;
            }
        if (pp->lS)
            {
            j=mxy[pp->x][pp->my+1]; qq=pnt.dat+j; pp->pS=j; qq->pN=i;
            j=abs(qq->x-pp->x)+abs(qq->y-pp->y);  pp->lS=j; qq->lN=j;
            }
        }
    }
//---------------------------------------------------------------------------
void A_star_graph::draw(Graphics::TBitmap *bmp)
    {
    int i;
    _pnt *p0,*p1;
    // init
    bmp->SetSize(xs,ys);
    // clear (walls)
    bmp->Canvas->Pen->Color=TColor(col_wall);
    bmp->Canvas->Brush->Color=TColor(col_wall);
    bmp->Canvas->FillRect(TRect(0,0,xs,ys));
    // space
    bmp->Canvas->Pen->Color=TColor(col_space);
    for (p0=pnt.dat,i=0;i<pnt.num;i++,p0++)
        {
        if (p0->pN>=0){ p1=pnt.dat+p0->pN; bmp->Canvas->MoveTo(p0->x,p0->y); bmp->Canvas->LineTo(p1->x,p1->y); }
        if (p0->pS>=0){ p1=pnt.dat+p0->pS; bmp->Canvas->MoveTo(p0->x,p0->y); bmp->Canvas->LineTo(p1->x,p1->y); }
        if (p0->pE>=0){ p1=pnt.dat+p0->pE; bmp->Canvas->MoveTo(p0->x,p0->y); bmp->Canvas->LineTo(p1->x,p1->y); }
        if (p0->pW>=0){ p1=pnt.dat+p0->pW; bmp->Canvas->MoveTo(p0->x,p0->y); bmp->Canvas->LineTo(p1->x,p1->y); }
        }
    // found path
    bmp->Canvas->Pen->Color=TColor(col_path);
    for (i=0;i<path.num;i++)
        {
        p0=pnt.dat+path.dat[i];
        if (!i) bmp->Canvas->MoveTo(p0->x,p0->y);
         else   bmp->Canvas->LineTo(p0->x,p0->y);
        }
    }
//---------------------------------------------------------------------------
void A_star_graph::compute(int p0,int p1)
    {
    _pnt *pp,*qq;
    int i,a,e;
    List<int> upd;  // list of vertexes to update
    // init
    path.num=0;
    if ((p0<0)||(p0>=pnt.num)) return;
    if ((p1<0)||(p1>=pnt.num)) return;
    // clear with max value
    for (pp=pnt.dat,i=0;i<pnt.num;i++,pp++) pp->a=0x7FFFFFFF;
    // init A* to fill from p1
    upd.allocate(xs+ys); upd.num=0;             // preallocate
    upd.add(p1); pnt[p1].a=0;                   // start from p1
    // iterative A* filling
    for (e=1;(e)&&(upd.num);)                   // loop until hit the start p0 or dead end
        {
        // process/remove last pnt in que
        pp=pnt.dat+upd[upd.num-1]; upd.num--;
        // link exist?                     compute cost    if less        update it                   reached p0?
        i=pp->pN; if (i>=0){ qq=pnt.dat+i; a=pp->a+pp->lN; if (qq->a>a) { qq->a=a; upd.add(i); } if (i==p0) { e=0; break; }}
        i=pp->pS; if (i>=0){ qq=pnt.dat+i; a=pp->a+pp->lS; if (qq->a>a) { qq->a=a; upd.add(i); } if (i==p0) { e=0; break; }}
        i=pp->pE; if (i>=0){ qq=pnt.dat+i; a=pp->a+pp->lE; if (qq->a>a) { qq->a=a; upd.add(i); } if (i==p0) { e=0; break; }}
        i=pp->pW; if (i>=0){ qq=pnt.dat+i; a=pp->a+pp->lW; if (qq->a>a) { qq->a=a; upd.add(i); } if (i==p0) { e=0; break; }}
        }
    // reconstruct path
    e=p0; pp=pnt.dat+e; path.add(e);
    for (;e!=p1;) // loop until path complete
        {
        a=0x7FFFFFFF; e=-1;
        // e = select link with smallest cost
        i=pp->pN; if (i>=0){ qq=pnt.dat+i; if (qq->a<a) { a=qq->a; e=i; }}
        i=pp->pS; if (i>=0){ qq=pnt.dat+i; if (qq->a<a) { a=qq->a; e=i; }}
        i=pp->pE; if (i>=0){ qq=pnt.dat+i; if (qq->a<a) { a=qq->a; e=i; }}
        i=pp->pW; if (i>=0){ qq=pnt.dat+i; if (qq->a<a) { a=qq->a; e=i; }}
        if (e<0) break; // dead end
        pp=pnt.dat+e; path.add(e);
        }
    }
//---------------------------------------------------------------------------
#endif
//---------------------------------------------------------------------------

and usage:

Graphics::TBitmap *maze=new Graphics::TBitmap;
maze->LoadFromFile("maze.bmp");
maze->HandleType=bmDIB;
maze->PixelFormat=pf32bit;
A_star_graph map;
map.ld(maze,0);
map.compute(0,map.pnt.num-1);
map.draw(maze);

The code is VCL based (using bitmap described in the second link) and I also use mine dynamic list template so:

List<double> xxx; is the same as double xxx[];
xxx.add(5); adds 5 to end of the list
xxx[7] access array element (safe)
xxx.dat[7] access array element (unsafe but fast direct access)
xxx.num is the actual used size of the array
xxx.reset() clears the array and set xxx.num=0
xxx.allocate(100) preallocate space for 100 items

Sorry not a python coder but think the code is straight forward enough ... so I was hopping you would have no problems to port/adapt to your environment.

Here output:

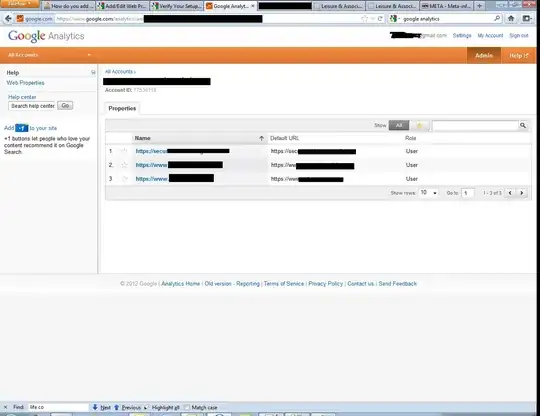
looks like it mimics yours... The code is still not optimized and can be improved more ... I think you should take closer look at the mx,my and mxy[][],myx[][] variables. Those are the topologicaly index sorted vertexes enabling the huge speedup against your code...

[Edit1]

I updated the A* search code (thx to Matt Timmermans) so here are updated results: