How to algorithmically find the biggest rectangle that can fit in a space with other rectangles?

Question

So I have a rectangle that is 6m x 2.25m and I have 4 other rectangles with static dimensions but are randomly placed inside the global rectangle.

I need to have a function that will calculate the area of the largest rectangle that can fit in the outer rectangle that also won't overlap with the other rectangles.

I thought about finding the maximum x distance between the small rects but depending if they're oriented landscape or portrait, x might not do the job. At this point I'm rather stuck and I can't find much online about doing this, but I'm sure this is quite an ordinary task for experienced coders.

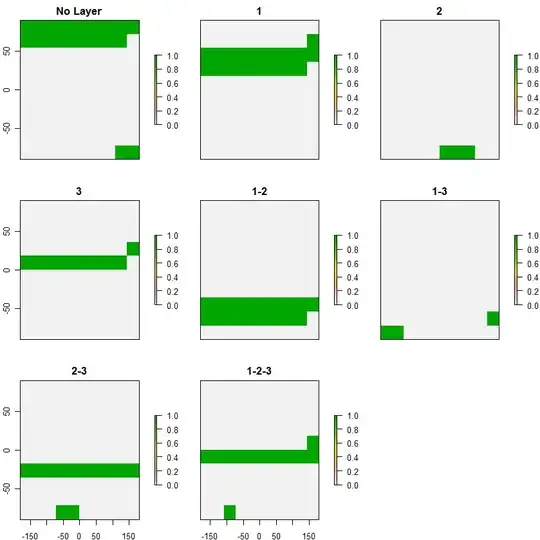
Update: Here an example image to show what I'm trying to describe. The colored rectangles are randomly placed with static dimensions, and I want to find the largest rectangle that can fit.

Thanks for your time!

Answer 1

As a starting point. Quadratic in the number of smaller rectangles in time and space complexity.

High-level approach

1) Divide the large rectangle into subrectangles based on the dimensions of the smaller subrectangles (purple lines in the figure). The optimal rectangle will always have its border made up of these subrectangles.

2) Mark off filled subrectangles that cannot be part of the end result (the red and yellow rectangles in the figure)

3) Now we have a search problem. We can use any search algorithm (I'm using a DFS). There are optimizations you can do on this (e.g. caching), but for simplicity:

Pseudocode

frontier = queue(all subrectangles)
largest_area = None

while frontier is not empty: 
    rectangle = pop a rectangle off frontier

    if all subrectangles to the right of rectangle are unoccupied:
        add (rectangle + extra subrectangles to the right) to frontier
        largest_area = max(area of new rectangle, largest_area)
    else if all subrectangles below rectangle are unoccupied:
        add (rectangle + extra subrectangles below) to the frontier
        largest_area = max(area of new rectangle, largest_area)

print largest_area

Explanation

Say rectangle is the green rectangle. The possible successor states are adding the subrectangles with blue stars or adding the subrectangles with pink stars. However the pink stars overlap with the yellow rectangle, so we cannot add that.

Answer 2

The optimal rectangle is such that it touches other rectangles on four sides (otherwise you can enlarge it). So you will restrict the search to the available coordinates.

A brute-force solution can work as follows:

• list all abscissas and ordinates (including the outer limits) and sort them increasingly;

• for every (abscissa, ordinate) combination, find the largest rectangle having this point as its top-left corner, as follows:

  • for every (abscissa', ordinate') combination such that abscissa' > abscissa and ordinate' > ordinate, use this point as the lower-right corner of the rectangle and test as follows:

    • for every given rectangle, check if it overlaps the rectangle under test; if there is an overlap, ignore this candidate.

    • if there were no overlaps, the candidate is accepted; compute its area and keep the largest so far.

For N rectangles, this process can take O(N^5) operations, so it is only usable for very small N.

---

You can speed up the process by replacing every abscissa, ordinate by its index and representing the rectangles in a bitmap. You paint every reduced rectangle in this bitmap.

Then when you want to test a candidate rectangle, try the longest run of empty pixels to the right; then try the next row and find the longest run of empty pixels which is not longer than the previous; and so on to the bottom of the bitmap (this ensures that you try all possible rectangles). Every time you try a rectangle, retrieve the original coordinates and compute the true area.

Below, the original rectangles, then the compressed bitmap representation and the pixels tried starting from the marked one (four rectangles are tried).

Answer 3

Here is my approach:

1. I divide to the subrectangles. Each subrectangle is object. Subrectangle declare to 2D array like in picture . https://i.stack.imgur.com/SHsJ1.png

   Want to do that, I use 2 sorted array without repeating elements:

   • (x_left_top and x_right_top)
   • (y_left_top and y_left_bottom)

   class Rectangle {
      constructor(left, top, width, height, area) {
               this.left = left;
               this.top = top;
               this.width = width;
               this.height = height;
               this.area = area;
      }
   }
   

2. So now we have array of subrectangles. And we need to set area for our rectangles. The occupy rectangle will set to -1.

   We can check if the rectangle is occupy or not with this function

   //rects is array of the colorful rectangle
   //rect1 is every rectangle in picture above.
   function isOverlap(rect1, rects){
       for (let i = 0; i < rects.length; i++) {
           if (rects[i].left <= rect1.left && 
               rect1.left < rects[i].left + rects[i].width &&
               rects[i].top <= rect1.top &&
               rect1.top < rects[i].top + rects[i].height)
           {
               return true;
           } 
       }
       return false;
   }
   

3. Now we have 2D array with rectangles and we know their area. If rectangle is not occupy, the rectangle area will have value height*width else the rectangle will set area to -1.

4. Now we have a problem # Maximum sum rectangle in a 2D matrix You can check the solution in geeksforgeeks