The point of this question is to show that ccf is giving wrong answers
I am writing a Shiny app. In one tab I want to plot the cross co-variance function using the ccf function from the stats package.
However, I found weird behavior in this function:
x <- rnorm(100)
y <- lag(x,-5) + rnorm(100)
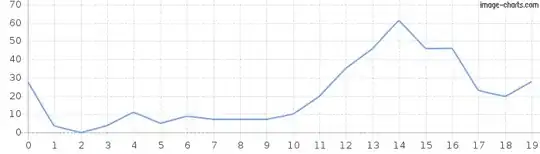
ccf(y, x, ylab='CCovF', type='covariance')
yields the correct cross co-variance function plot:
However, I changed the type of y and the plot was then wrong:
y <- as.numeric(y)
ccf(y, x, ylab='CCovF', type='covariance')
Does someone have any idea what is happening ? What is causing this behavior and how to remedy it ?
In the app the y input will not have the tsp attribute and it will be just a numeric type.
This is actually the most important part of the question, the fact that the y input will have a numeric type and not an atomic type.
I tried using lag() on y to make it gain back its attribute, but the function still didn't work:
ccf(lag(y,0), x, type = "covariance")

If this function only gives a correct answer if the y series is written intentionally a lag of the x series and not when it is naturally a lag of then x series then this function serves nothing in the real life.

 ]
]