How to find the point on an edge which is the closest point to another point

Question

I'm searching the way to efficiently find the point on an edge which is the closest point to some other point.

Let's say I know two points which are vertices of the edge. I can calculate the equation of the line that crosses those points.

What is the best way to calculate the point on the edge which is the closest point to some other point in the plane.

I would post an image but I don't have enough reputation points.

Answer 1

Let’s assume the line is defined by the two points (x1,y1), (x2,y2) and the “other point” is (a,b). The point you’re looking for is (x,y).

You can easily find the equation of the black line. To find the blue line equation use the fact that m1*m2=-1 (m1 and m2 are the slopes of the two lines).

Clearly, the point you’re looking for is the intersection between the two lines.

There are two exceptions to what I was saying:

1. If x1=x2 then (x,y)=(x1,b).
2. If y1=y2 then (x,y)=(a,y1).

The following Python function finds the point (if you don’t know Python just think of it as a psudo-code):

def get_closest_point( x1,y1, x2,y2, a,b ):
    if x1==x2: return (x1,b)
    if y1==y2: return (a,y1)
    m1 = (y2-y1)/(x2-x1)
    m2 = -1/m1
    x = (m1*x1-m2*a+b-y1) / (m1-m2)
    y = m2*(x-a)+b
    return (x,y)

Answer 2

You have three zones to consider. The "perpendicular" approach is for the zone in the middle:

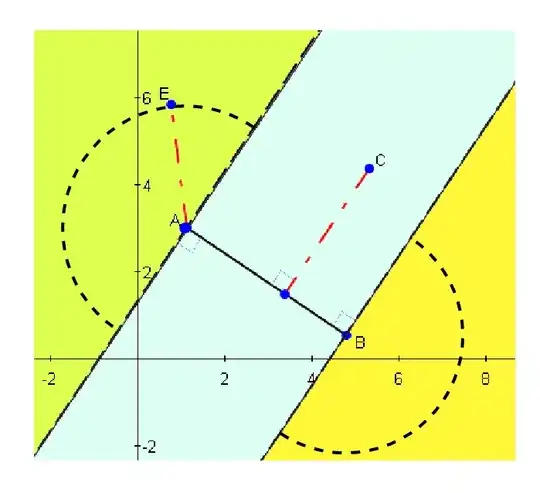
For the other two zones the distance is the distance to the nearest segment endpoint.

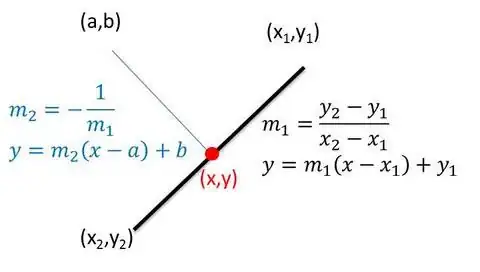
The equation for the segment is:

y[x] = m x + b

Where

  m -> -((Ay - By)/(-Ax + By)), 
  b -> -((-Ax By + Ay By)/(Ax - By))  

And the perpendiculars have slope -1/m

The equations for the perpendicular passing thru A is:

  y[x] = (-Ax + By)/(Ay - By) x + (Ax^2 + Ay^2 - Ax By - Ay By)/(Ay - By)

And the perpendicular passing thru B is the same exchanging the A's and B's in the equation above.

So you can know in which region lies your point introducing its x coordinate in the above equations and then comparing the y coordinate of the point with the result of y[x]

Edit

How to find in which region lies your point?

Let's suppose Ax ≤ Bx (if it's the other way, just change the point labels in the following formulae)

We will call your point {x0,y0}

1) Calculate

 f[x0] =  (-Ax + By)/(Ay - By) x0 + (Ax^2 + Ay^2 - Ax By - Ay By)/(Ay - By)

and compare with y0.

If y0 > f[x0], then your point lies in the green field in the figure above and the nearest point is A.

2) Else, Calculate

g[x0] =  (-Bx + Ay)/(By - Ay) x0 + (Bx^2 + By^2 - Bx Ay - By Ay)/(By - Ay)  

and compare with y0.

If y0 < g[x0], then your point lies in the yellow field in the figure above and the nearest point is B.

3) Else, you are in the "perpendicular light blue zone", and any of the other answer tell you how to calculate the nearest point and distance (I am not going to plagiarize :))

HTH!

Answer 3

I can describe what you want to do in geometric terms, but I don't have the algorithm at hand. Will that help?

Anyway, you want to draw a line which contains the stray point and is perpendicular to the edge. I think the slopes are a negative inverse relation between perpendicular lines, if that helps.

Then you want to find the intersection of the two lines.

Answer 4

Let's stick with the 2D case to save typing. It's been a while, so please forgive any elementary mistakes in my algebra.

The line forming the edge between the two points (x1, y1), (x2, y2) is represented as a function

y = mx + b

(You get to figure out m and b yourself, but it's elementary)

What you want to do is minimize the distance from your point (p1, p2) to a point on this line, i.e.

(p1-x)^2 + (p2-y)^2     (equation I)

subject to the equation

y = mx + b              (equation II)

Substitute equation II into equation I and solve for x. You'll get two solutions; pick the one which gives the smaller value in equation I.