Partially factoring an expression in Sympy

Question

Suppose I have an expression of the form 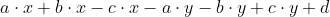. I know that I can simplify the expression like so: 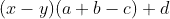. However, sympy.simplify and sympy.factor both return the original expression.

To work around this, I've been operating on the expression at a low level:

factor_map = defaultdict(set)
additive_terms = expr.as_coeff_add()[-1]
for term1, term2 in combinations(additive_terms, 2):
    common_terms = (
        set(term1.as_coeff_mul()[-1])
        & set(term2.as_coeff_mul()[-1])
    )
    if common_terms:
        common_factor = sympy.Mul(*common_terms)
        factor_map[common_factor] |= {term1, term2}

factor_map now looks like so:

{
    a: {a⋅x, -a⋅y}, 
    b: {b⋅x, -b⋅y}, 
    c: {-c⋅x, c⋅y}, 
    x: {a⋅x, b⋅x, -c⋅x}, 
    y: {-a⋅y, -b⋅y, c⋅y}
}

I sort it by the number of operations represented by the terms:

factor_list = sorted(
    factor_map.items(),
    key = lambda i: (i[0].count_ops() + 1) * len(i[1])
)[::-1]

I then just rebuild the expression:

used = set()
new_expr = 0
for item in factor_list:
    factor = item[0]
    appearances = item[-1]
    terms = 0
    for instance in appearances:
        if instance not in used:
            terms += instance.as_coefficient(factor)
            used.add(instance)
    new_expr += factor * terms
for term in set(additive_terms) - used:
    new_expr += term

This gives new_expr = d + x*(a + b - c) + y*(-a - b + c). Not great, but better.

I can also improve on this by dividing each combination of additive terms by each other, checking if the result is a number, and using that information to further reduce the output to new_expr = d + (x - y)*(a + b - c).

I've also tried to apply sympy.factor to every possible combination of additive terms, but obviously that blows up very quickly for any reasonably big expression.

---

Edit: Here's an implementation that uses sympy.factor on all partitions of the set of additive terms (partitions function borrowed from this answer):

def partition(collection):
    if len(collection) == 1:
        yield [ collection ]
        return

    first = collection[0]
    for smaller in partition(collection[1:]):
        # insert `first` in each of the subpartition's subsets
        for n, subset in enumerate(smaller):
            yield smaller[:n] + [[ first ] + subset]  + smaller[n+1:]
        # put `first` in its own subset 
        yield [ [ first ] ] + smaller


def partial_factor(expr):
    args = list(expr.as_coeff_add()[-1])
    # Groupings is just a cache to avoid duplicating factor operations
    groupings = {}

    unique = set()

    for p in partition(args):
        new_expr = 0
        for group in p:
            add_group = sympy.Add(*group)
            new_expr += groupings.setdefault(add_group, sympy.factor(add_group))
        unique.add(new_expr)
    return sorted(unique, key=sympy.count_ops)[0]

For an expression like a*x + b*y + c*z + d + e*x + f*y + h*z, it takes 7.8 seconds to run on my computer, whereas the other method takes 378 microseconds and gives the same result. Seems like there should be a way to be more rigorous than the first method without taking 20,000 times longer to solve it.

---

I feel like it shouldn't be this hard to get what I want. Is there an easier way to do this?

Answer 1

This similar question has an answer involving the func parameter to collect(). It seems to work in this particular case as well, although you have to explicitly mention d:

from sympy import *
a, b, c, d, x, y = symbols('a, b, c, d, x, y')
expr = a * x + b * x - c * x - a * y - b * y + c * y + d
collect(expr, d, func=factor)
=> d + (x - y)*(a + b - c)

This helps in this specific case, however a more general and automatic solution does not exist.

Also I could not find any documentation for this func parameter anywhere, other than it existing.

Github issue tracking this problem

Answer 2

It's hard to suggest a strategy of "partial factoring" that works most of the time. Here is a thing to try, devised with your example in mind (a polynomial of several variables).

Given an expression: Attempt to factor it. If unsuccessful, look at the coefficient of each symbol that it contains; the method Expr.coeff(Symbol) does that. The symbol with the smallest coefficient (measured by the number of symbols contained) is considered an obstacle to factoring and is removed from the expression. Repeat.

This logic is encoded below, and partial_factor(a*x + b*x - c*x - a*y - b*y + c*y + d) does return d + (x - y)*(a + b - c).

def partial_factor(expr):
    to_factor = expr
    non_factorable = 0
    while to_factor != 0:
        if factor(to_factor) != to_factor:
            return factor(to_factor) + non_factorable
        coeffs = {v: to_factor.coeff(v) for v in to_factor.free_symbols}
        min_size = min([len(coeffs[v].free_symbols) for v in coeffs])
        for v in coeffs:
            if len(coeffs[v].free_symbols) == min_size:
                non_factorable += v*coeffs[v]
                to_factor -= v*coeffs[v]
                break
    return expr

Answer 3

@butterwagon: I tested your work around and found that it fails for expressions like x + 1, where it returns just x. To solve that I'd recommend to change the line

additive_terms = expr.as_coeff_add()[-1]

to

const, additive_terms = expr.as_coeff_add()

and add const to the final result:

new_expr += const