8

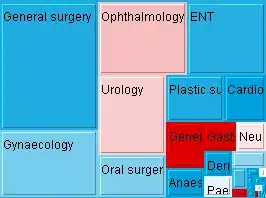
Here is the problem. I have rectangular canvas that have size of 1. So it have coordinate sistem of (0.0 ... 1.0 - x and 0.0 ... 1.0 - y).

I also have some tiles. Tiles are also rectangles. They have diffrent size and amount of tiles is a variable.

I want to stack tiles in rectangular canvas, from 0.0 to 1.0 (from left to right, from top to bottom):

1) tiles have to fit in canvas (but fill as much space as they could)

2) tiles have to be scaled (if they don't fit), each tile should be scaled by the same amount (they have to remain same proportions).

3) imagine that you have this 'tiles' in your hand, and you placing them into this canvas one after another

4) it almost like "TreeMap algorithm" but - shape of tiles have to be the same (rectangles) and i don't need to fill all space of canvas

here is what i want to get

Is there anybody who can show me an algoritm in any C alike language (C, C++, Java, C#)?

*I tried this.

1) i calculated area of tile, then i calculate a sum of tile's areas (for example: i have two tiles, one have area of 2, other area of 1, them it's mean i have total sum of 3)

2) then i calculate what "proportion" each tile have in "total sum of areas" (for example: 2/3 and 1/3)

3) then calculate size of rectangle tile by Math.sqrt(x) (for example: Math.sqrt(2/3))

4) then draw tile one by one...

But this dosen't work always. Sometimes i get tiles to be out of canvas..*

obenjiro
  • 3,665
  • 7
  • 44
  • 82
  • 2
    You don't give any criteria for optimization. One algorithm would be to line up the tiles horizontally in a single row with tops aligned, then scale the row so the tallest tile and the sum of the tile widths are <= 1. – Ted Hopp Mar 07 '11 at 15:41
  • well.. i will repeat my self _I want to **stack** tiles in rectangular canvas, from 0.0 to 1.0 (from left to right, from top to bottom)_ – obenjiro Mar 07 '11 at 16:03
  • Your example is confusing as is your description. It doesn't seem like you're stacking things at all. Maybe the word doesn't mean what you think it means. Plus, @Ted's right. Just shrink all your tiles down to an infinitesimally small proportion and then line them up. Without an optimization function, that's perfectly legit. – Mark Peters Mar 07 '11 at 16:12
  • The picture is preatty ugly :) I just want to put tiles inside rectangle canvas, i want to fill as much space as i can and also save tiles proportions.. how can i say this simplier? – obenjiro Mar 07 '11 at 16:16
  • Suggestion for additional criteria: you want to fill as much space as you can, and each tile should be scaled by the same amount. Does that sound sensible? – Thomas Mar 07 '11 at 16:23
  • @Ai_boy: Your latest edit made it more clear. But what are the rules for left-to-right/up-to-down, and what is its priority relative to using as much space as possible? For example, in your second example, you could scale the squares down less if you arranged the orange squares vertically instead. We need to have a function that incorporates that relative priority. – Mark Peters Mar 07 '11 at 16:24
  • @Thomas yes, it's more acurate discription... – obenjiro Mar 07 '11 at 16:27
  • One important thing that i can't control order of rectangle.. for example.. In second example first one was Big rectangle, then was Small... i put small recntagle next to big (in right corner), so the second Big rectangle now can't be placed (in right corner).. so i put Big one in bottom, and Small one ones again (in right corner). Just imagine that you have this rectangles in your hand. And you placing them one after another.. – obenjiro Mar 07 '11 at 16:32
  • What have you tried so far? If you are stuck, could you simplify the problem? Maybe solving a simple version of this problem will give you insight on how to solve your problem. – David Weiser Mar 07 '11 at 16:54
  • @David I add some descriprion of what i have tried so far at the bottom of the question... – obenjiro Mar 07 '11 at 17:18
  • @ted-hopp What do you mean by "criteria for optimization"? – obenjiro Mar 08 '11 at 08:41
  • Interesting problem. I think I will try to edit your description a little. Hopefully you find the edits acceptable. – Fantius Mar 10 '11 at 13:57
  • The entire question is effectively: "I have a set of rectangular tiles of varying size. I wish to place them in a rectangular container (without overlap) such that the filled-area percentage is maximized. All tiles must be used." – Fantius Mar 10 '11 at 14:08
  • @Fantius Tnx a lot, your 'description' is really more accurate :) – obenjiro Mar 10 '11 at 19:45
  • Are all your tiles squares and is the container also a square? Your examples (and your described attempt) only include square tiles and a square container. – mhum Mar 12 '11 at 04:17
  • Yes.. and this is a problem.. i can't fully cover square container with square tiles, but i want to cover as much space as possible.. – obenjiro Mar 12 '11 at 12:20
  • I still don't understand the question. The second example looks like you're scaling the tiles down in order to fit them into the rectangle, yet the description mentions nothing about scaling. What are the parameters the algorithm is expected to set? Scale factor per tile? Positions of each tile? – Adrian McCarthy Mar 14 '11 at 18:48
  • look at the description.. i returned to more detaild desctiption.. – obenjiro Mar 15 '11 at 19:11

5 Answers5

4

It may appear that this is a packing problem, however if we try to solve this problem exactly as it described it is not. In other words there is no solution because, again, there is no problem in a question as it is described. If we have ONLY ONE box and fixed set of tiles and requirement that they ALL must fit into box there is no room for optimization. I can see several related optimization problems:

1. Given fixed set of tiles that must be packed into boxes of same or different sizes find optimal packing order so that minimal number of boxes is used.

2. Given single box of an arbitrary size and set of tiles find optimal (maximum) set of tiles that can be fit into a box.

3. Given a box and set of tiles - answer the question if it is possible to fit them into a box or not.

Which one of these are you trying to solve?

The way problem is set right now is meaningless, because no matter which order you place the tiles in the box they will always use same amount of space no matter how they are arranged, as soon as they all fit in of course.

Alexei Polkhanov
  • 599
  • 4
  • 8
  • I have a set of rectangular tiles of varying size. I wish to place them in a rectangular container (without overlap) such that the filled-area percentage is maximized. **All tiles must be used. Tiles count is variable.** – obenjiro Mar 12 '11 at 20:14
  • Tile will either fit into container or they will not. In case if all tiles fit into a container they will take exactly same amount of space no matter how you arrange them.
    Are you trying to find arrangement of tiles in a box such that it leaves maximum possible square area of free space? It is like when you solve problem No 3. by adding larger and smaller size tile to the set till you find size of largest tile that can be added to a set and still fit inside a box without overlaps. Changing size of that tile should be done in a same manner as you do in binary search.     – Alexei Polkhanov Mar 12 '11 at 22:21
  • yes.. i want all tiles to fit into container, but for example, i have three big tiles, if put two of them into the first row, and one into the second row THEN they take more space of 'recntangular' container, more than if i put all three tiles into the one row.. so.. it is matter how to arrange them... and this is the problem – obenjiro Mar 12 '11 at 23:15
  • I this case you may want to read this for a description of an algorithm that can be combined with binary search for maximum free space. http://www.combinatorics.org/Surveys/ds7.html – Alexei Polkhanov Mar 12 '11 at 23:38
  • It's not like you solve my problem but at list you gave me some idias.. tnx – obenjiro Mar 14 '11 at 06:52
2

Try a monte-carlo algorithm:

Repeat until result is good enough or until you aren't seeing any improvement
  Select (with removal) a random first tile
  Place the first tile at a random position
  Repeat until no remaining tiles
    Select (with removal) a random tile
    Place it adjoining to the existing "tile blob" 
      (you might have to do a search here to find the best place to plug it in)
  Check to see if you have a new best filled-area percentage

All random tile selections should be weighted by the tile's area so that you tend to place the larger ones first.

Fantius
  • 3,806
  • 5
  • 32
  • 49
2

I don't think this is a (bin)-packing problem because I wrote one for the 1D bin-packing problem. I think the problem here is solved by the 2D-cutting-stock problem, maybe there is also a 2D-bin-packing. What you want is to try the knappsack-problem too. This problem is hard to solve (NP) and there is no solution. It's a bit like the Travelsalesman problem where the number of solution is exponential to the number of cities. If you can reduce the ccomplexity to a 1D problem you may try my bin-packing algorithm at phpclasses.org.

Micromega
  • 12,486
  • 7
  • 35
  • 72
  • Actually there are two bin packing classes there, the Bin Packer was applied to fit files in disk containers of the same size: http://www.phpclasses.org/binpacker . The Bin Packing implements the Ant-Colony-Optimization bin-packing solver: http://www.phpclasses.org/bin-packing – mlemos Mar 13 '11 at 21:50
  • I think it is bin packing problem in combination to binary search. You just have to add extra square to a set of squares and then keep changing its size in a binary search manner till you find the maximum square of free space. Think of it as a task of optimizing location for furniture in a room so that you have maximum square space your cat/kid can play within. – Alexei Polkhanov Mar 13 '11 at 23:27
  • @Alexei: If you mean this http://www.combinatorics.org/Surveys/ds7.html then it is not easy to solve and similar to 2D-cutting-stock and also this question is looking like homework! – Micromega Mar 15 '11 at 02:13
1

As others pointed - problem description is not very clear. But i'm assuming that you can scale each tile as you need (at least your examples shows that tile scaling is possible). So my solution will be simple (but maybe not what you want nor optimal):

  • Scale each tile by factor : 
    EDGEspace / (EDGEtile * N ½)
  • Place each tile in current row, if tile gets out of space limits - advance to next row.

Here N is nearest perfect square greater or equal to the total number of tiles.

p.s. If you need some spacing between tiles - just make above scale factor a little bit smaller.

Hope that helps.

Agnius Vasiliauskas
  • 10,935
  • 5
  • 50
  • 70
  • 1
    what dose EDGE mean in your formula? – obenjiro Mar 16 '11 at 14:24
  • Edge == Width. EDGE(space) is width of your canvas and Edge(tile) is width of current tile. (Actually if you have rectangles instead of squares then Edge==Max(width,height). That is we approximating rectangle to bigger square). But my solution violates your new (2) requirement of 'keeping same proportions of tiles', because it re-scales all tiles to the same size ... – Agnius Vasiliauskas Mar 16 '11 at 19:40
0

I am not sure if it's what you want but you can look at TreeMap algorithm.

TreeMap

Wikipedia definition

C++ implementation

Absolom
  • 1,369
  • 1
  • 13
  • 28
  • Nope.. shape of tiles have to be the same (rectangles). In your example shape changes.. – obenjiro Mar 07 '11 at 16:34
  • 1
    You are right... [Treemapping with a given aspect ratio](http://stackoverflow.com/questions/5129221/treemapping-with-a-given-aspect-ratio) – Absolom Mar 07 '11 at 16:39
  • 1
    `4) it almost like "TreeMap algorithm" but - shape of tiles have to be the same (rectangles) and i don't need to fill all space of canvas` – obenjiro Mar 07 '11 at 16:43
  • run the treemap algorithm, then shrink each rectangle till it has the correct proportions for its tile (equivalent to scaling the tile down) – Martin DeMello Mar 16 '11 at 15:23