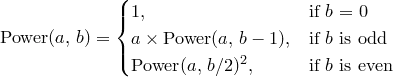I implemented this function power() which takes two arguments a and b and computes ab.
typedef long long int LL;
LL power(int a,int b)
{
int i = 1;
LL pow = 1;
for( ; i <= b ; ++i )
pow *= a;
return pow;
}
Given : ab falls in the range of long long int.
Problem : How to reduce the time complexity of my algorithm?