Advice:
- use
np.fft.fft
- fft starts at 0 Hz
- normalize/rescale
Complete example:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
def norm_fft(y, T, max_freq=None):
N = y.shape[0]
Nf = N // 2 if max_freq is None else int(max_freq * T)
xf = np.linspace(0.0, 0.5 * N / T, N // 2)
yf = 2.0 / N * np.fft.fft(y)
return xf[:Nf], yf[:Nf]
def generate_signal(x, signal_gain=10.0, noise_gain=0.0):
signal = norm.pdf(x, 0, 1)
noise = np.random.randn(x.size)
return signal_gain * signal + noise_gain * noise
# Signal parameters
x1 = 0.0
x2 = 5.0
N = 10000
T = x2 - x1
# Generate signal data
x = np.linspace(x1, x2, N)
y = generate_signal(x)
# Apply FFT
xf, yf = norm_fft(y, T, T / np.pi)
# Plot
fig, ax = plt.subplots(2)
ax[0].plot(x, y)
ax[1].plot(xf, np.abs(yf))
plt.show()
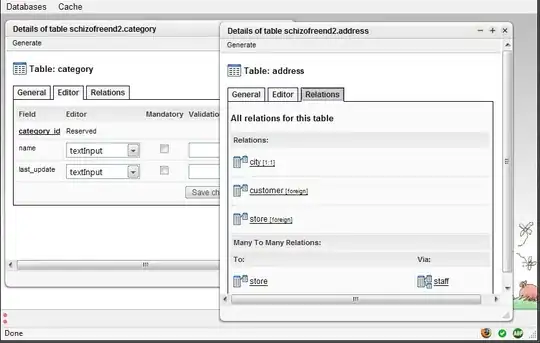
Or, with noise:
Plots with symmetry
Alternatively, if you want to enjoy the symmetry in the frequency domain:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
def norm_sym_fft(y, T, max_freq=None):
N = y.shape[0]
b = N if max_freq is None else int(max_freq * T + N // 2)
a = N - b
xf = np.linspace(-0.5 * N / T, 0.5 * N / T, N)
yf = 2.0 / N * np.fft.fftshift(np.fft.fft(y))
return xf[a:b], yf[a:b]
def generate_signal(x, signal_gain=10.0, noise_gain=0.0):
signal = norm.pdf(x, 0, 1)
noise = np.random.randn(x.size)
return signal_gain * signal + noise_gain * noise
# Signal parameters
x1 = -10.0
x2 = 10.0
N = 10000
T = x2 - x1
# Generate signal data
x = np.linspace(x1, x2, N)
y = generate_signal(x)
# Apply FFT
xf, yf = norm_sym_fft(y, T, 4 / np.pi)
# Plot
fig, ax = plt.subplots(2)
ax[0].plot(x, y)
ax[1].plot(xf, np.abs(yf))
plt.show()
Or, with noise: